Page 20 - 2023年第54卷第3期

２．２ 流变模型
２．２．１ 本构关系 堆积层滑坡是山区水库滑坡的主要类型之一，该类滑坡主要由碎石与砂土的混合物
组成，在滑动时具有流体运动的特征。根据 Ｈｕｎｇｒ和 Ｄｏｕｇａｌｌ提出的等效流体假设 ［１９］ ，可将这类复杂、
非均质的滑坡简化 成单一 物质 组成 的流体，且其内 部的剪 切 变 形 速 度 与 剪 切 应 力 之 间 为 非 线 性 关
系 ［２４］ ，故可采用 Ｈｅｒｓｃｈｅｌ － Ｂｕｌｋｌｅｙ模型对滑坡运动（流动）特征进行描述，其方程为：
ｎ
·γ＋ τ ｙ
τ ＝ η ０ （５）
２ － １
式中：τ 为剪切应力，Ｐａ；η ０ 为黏性系数，Ｎ·ｓ?ｍ ；γ为剪切变形速度，ｓ ；ｎ为流变指数；τ ｙ 为屈
＞０时代表宾
服应力，Ｐａ。显然，上式中当 ｎ ＝ １ 且 τ ｙ ＝ ０ 时代表牛顿流体的运动特征，而当 ｎ ＝ １且 τ ｙ
汉流体的运动特征。
有研究表明，宾汉流体模型用于预测土体大变形时可有效描述土体初始流动破坏和形态演化过
程 ［２５ － ２６］ 。但是该模型中的黏性系数依存于剪应变率，即随着剪切变形速度变化而变化，故引入等效牛
顿流体黏性系数的概念，将宾汉流体模型与牛顿流体模型之间建立如下关系：
＝
·γ ＋ τ ｙ η ′·γ （６）
τ ＝ η ０
由式（６）可得到等效黏性系数 η ′的表达式为：
τ ｙ
＋ （７）
η ′ ＝ η ０
γ
２
式中：η ′为等效黏性系数，Ｎ·ｓ?ｍ 。由式（７）可以看出，当剪切应力不变，且剪切变形速度趋于零
，
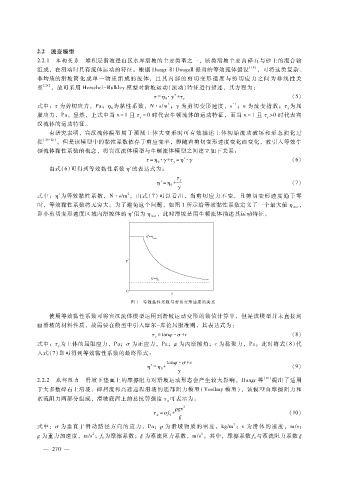
时，等效黏性系数将无穷大。为了避免这个问题，如图 １所示给等效黏性系数定义了一个最大值 η ｍａｘ
，此时滑坡是用牛顿流体描述其运动特征。
即小剪切变形速度区域内滑坡体的 η ′值为 η ｍａｘ

图 １ 等效黏性系数与剪切变形速度的关系

使用等效黏性系数可将宾汉流体模型运用到滑坡运动变形的数值计算中，但是该模型并未直接刻
画滑坡的材料性质，故需要在模型中引入摩尔－ 库伦屈服准则，其表达式为：
＝ ｔａｎ φ ·σ ＋ ｃ （８）
τ ｙ
为土体的屈服应力，Ｐａ；σ为正应力，Ｐａ；φ为内摩擦角；ｃ为黏聚力，Ｐａ。此时将式（８）代
式中：τ ｙ
入式（ ７）即可得到等效黏性系数的最终形式：
ｔａｎ φ ·σ ＋ ｃ
＋ （９）
η ′ ＝ η ０
γ
２．２．２ 底部阻力 滑坡下垫面上的摩擦阻力对滑坡运动形态会产生较大影响。Ｈｕｎｇｒ等 ［１８］ 提出了适用
于大多数碎石土滑坡、碎屑流和高速远程滑坡的底部阻力模型（ Ｖｏｅｌｌｍｙ模型），该模型由摩擦阻力和
可表示为：
紊流阻力两部分组成，滑坡底面上的总抗剪强度 τ ｗ
２
ρ ｇｖ
τ ｗ σ ｆ ＋ （１０）
＝
０
ξ
３
式中：σ为垂直于滑动路径方向的应力，Ｐａ；ρ 为滑坡物质的密度，ｋｇ?ｍ ；ｖ为 滑体 的速 度，ｍ?ｓ；
２ ２
ｇ为重力加速度，ｍ?ｓ；ｆ为摩擦系数；ξ 为紊流阻力系数，ｍ?ｓ。其中，摩擦系数 ｆ与紊流阻力系数 ξ
０ ０
０
— ２ ７ —