Page 55 - 2025年第56卷第6期
P. 55
3.2.2 河道平衡输沙的不淤流速 河相关系将 U 视为是第 4 个关键未知量,需寻找 U 与来水来沙的函
数关系,使方程式封闭。根据河相关系式(11)(13)求解,代入流量连续方程 U = Q/A = Q/ ( RB),可得
到输沙不淤流速公式:
0.269 Q 0.081 (18)
U c = 2.037S v
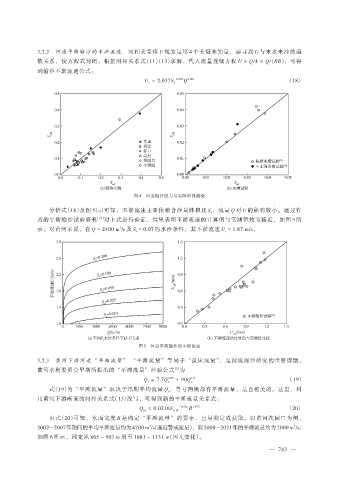
图 4 河道输沙能力与实际资料检验
分析式(18)及图 5(a)可知,不淤流速主要依赖含沙量体积比 S ,流量 Q 对 U 的影响较小。通过作
v
者的平衡输沙试验资料 [23] 对上式进行验证,结果表明不淤流速的计算值与实测值较为接近,如图 5 所
示。对黄河来说,在 Q = 2400 m /s 及 S = 0.07 的水沙条件,其不淤流速 U = 1.87 m/s。
3
c
v
图 5 河道平衡输沙的不淤流速
3.2.3 黄河下游河道“平滩流量” “平滩流量”等同于“造床流量”,是河流泥沙研究的重要课题。
[2]
黄河水利委员会早期所提出的“平滩流量”经验公式 为
0.85 1/3 (19)
Q z = 7.7Q x + 90Q x
式(19)为“平滩流量”取决于汛期平均流量 Q ,等号两侧都有平滩流量,是自相关的。这里,利
x
用黄河下游断面的河相关系式(13)改写,可得到新的平滩流量关系式:
Q bf = 0.0216S -0.036 B 1.795 (20)
v,bf
由式(20)可知,水面宽度 B 是确定“平滩流量”的要素,且易测定或获取。以黄河花园口为例,
2002—2007年期间的平均平滩流量约为4700 m /s(逼近警戒流量),而2008—2021年的平滩流量约为7000 m /s,
3
3
如图 6 所示,河宽从 865 ~ 907 m 增至 1081 ~ 1131 m(因 S 变化)。
v
— 743 —