Page 66 - 2025年第56卷第6期
P. 66
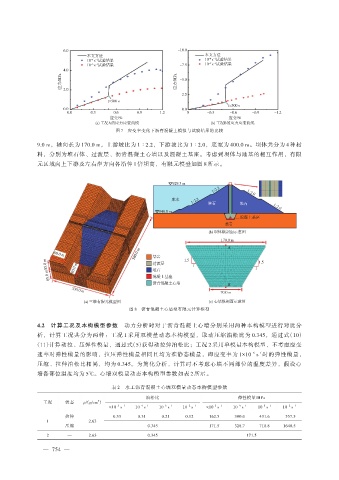
图 7 应变率变化下沥青混凝土模拟与试验结果的比较
9.0 m,轴向长为 170.0 m,上游坡比为 1∶2.2,下游坡比为 1∶2.0,底宽为 400.0 m。坝体共分为 4 种材
料,分别为堆石体、过渡层、沥青混凝土心墙以及混凝土基座。考虑到坝体与地基的相互作用,有限
元区域向上下游及左右岸方向各沿伸 1 倍坝高,有限元模型如图 8 所示。
图 8 沥青混凝土心墙坝有限元计算模型
4.2 计算工况及本构模型参数 动力分析时对于沥青混凝土心墙分别采用两种本构模型进行对比分
析,计算工况共分为两种:工况 1 采用双模量动态本构模型,取动压缩泊松比为 0.345,通过式(10)
(11)计算动拉、压弹性模量,通过式(5)获得动拉伸泊松比;工况 2 采用单模量本构模型,不考虑应变
速率对弹性模量的影响,拉压弹性模量相同且均为准静态模量,即应变率为 1×10 s 时的弹性模量,
-1
-5
压缩、拉伸泊松比相同,均为 0.345。为简化分析,计算时不考虑心墙不同部位的温度差异,假设心
墙各部位温度均为 5℃。心墙双模量动态本构模型参数如表 2 所示。
表 2 水工沥青混凝土心墙双模量动态本构模型参数
泊松比 弹性模量/MPa
工况 状态 ρ/(g/cm )
3
-5 -1 -4 -1 -3 -1 -2 -1 -5 -1 -4 -1 -3 -1 -2 -1
≤10 s 10 s 10 s 10 s ≤10 s 10 s 10 s 10 s
拉伸 0.33 0.31 0.21 0.12 162.5 300.0 431.6 557.5
1 2.63
压缩 0.345 171.5 328.7 710.8 1640.5
2 — 2.63 0.345 171.5
— 754 —