Page 34 - 2025年第56卷第11期

工装备和施工参数要求较为严格。置换率根据式（1）计算得到，并经计算或试验校核，为了显著提高
碎石桩处理地基的承载力，需要 0.25 或更大的面积置换率 ［34-35］ 。
现行振冲相关规范 ［36］ 中给出了等边三角形、方形及矩形 3 种不同布桩形式的置换率计算方法，主要
是基于等效影响圆直径，并不能体现布桩型式影响的本质特征。本文从间排距的本质特征给出新的计算
方法如下。图 4 为桩体布置模式表征示意图，分别用 S p 、S r 、θ 表征桩间距、桩排距和错位角，定义间排
距比 η = S p /S r 。S p 、η、θ 确定的唯一三角形 O 1 O 2 O 3 （下文记 △O 1 O 2 O 3 ）是组成布桩平面的最小单元。矩形

布桩、正方形布桩、等边三角形布桩分别是 θ = 90°、θ = 90°且 η = 1、θ = 60°且 η = 2/ 3 的特殊情况。
基于本文的布桩模式（图 4），置换率计算公式见式（3），可知置
换率 m 不受错位角 θ 影响，只与桩间距 S p 和间排距比 η 有关。其中

4
分母上的常数 ≈1.13，即为规范中正方形和矩形布桩下等效影
π
响圆直径计算公式中的系数 ［36］ 。
π
2
d 0 η 2
8 d 0
m = = （3）
1 ( ) 2 S p 2
S p S r 4
2 π
图 4 碎石桩体布置模式表征示意
式中 d 0 为桩径。
为了定量评价布桩模式的影响及最佳形状，本文提出以桩间土与最近碎石桩距离的最大值 d s 作为
布桩模式的评价指标，如式（4）所示。由于△O O O 是组成布桩平面的最小单元，分析△O O O 区域内
1 2 3 1 2 3
的 d 即可反应整体情况。d s 是影响施工期土体挤密和振密、运行期桩间土排水固结和消散孔压的主要
s
因素，d s 越小，施工期振冲器对土体的挤密或振密作用越大、运行期桩间土排水路径越短。
d s = max min d( s，p) |p ∈ { O 1 ，O 2 ，O 3 } |s ∈ △O 1 O 2 O 3) （4）
( (
)

式中：d s 为桩间土到最近碎石桩距离的最大值；max（）、min（）分别为取最大值和最小值函数；d (s，p)
为 s 与 p 之间的水平距离，s 为△O O O 内任意点，p 为△O O O 的顶点。
1 2 3 1 2 3
根据三角形的性质和 d s 的定义，当 △O 1 O 2 O 3 为锐角三角形时，d s 等于其外接圆半径 R ；当
△O 1 O 2 O 3
π
△O 1 O 2 O 3 为钝角三角形时（∠O 1 > ，△O 1 O 2 O 3 中只有 ∠O 1 可能是钝角），d s 等于 △O 1 O 2 O 4 外接圆半径
2
R 和 △O 1 O 3 O 4 外接圆半径 R 中的较大值。d s 按照式（5）计算。
△O 1 O 2 O 4 △O 1 O 3 O 4
ì ì ü ü ï ï ï ï ï ï ï ï
ï ï
ï ï
d s = min í S p ，max í S p ， S p ý ý （5）

î
ï ï 2 cos [ θ - arctan (η - cot θ ) ] ï ï η sin 2θ η sin [ 2 arctan ( η - cot θ ) þ þ ï ï ï ï ]
î
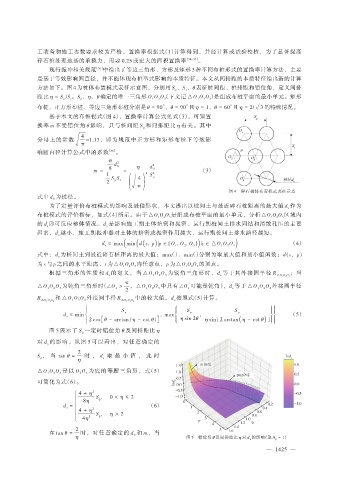
图 5 展示了 S p 一定时错位角 θ 及间排距比 η
对 d s 的影响。从图 5 可以看出，对任意确定的
2
S p ， 当 tan θ = 时 ， d s 取 最 小 值 ， 此 时
η
△O 1 O 2 O 3 是以 O 2 O 3 为底的等腰三角形，式（5）
可简化为式（6）。
ì 4 + η 2
ï ï S p ， 0 < η ≤ 2
ï ï 8η
d s = í （6）
ï ï 4 + η 2
ï ï 4η 2 S p ， η > 2
î
2
在 tan θ = 时，对任意确定的 d 0 和 m，当
η 图 5 错位角 θ 及间排距比 η 对 d s 的影响（取 S p = 1）
— 1425 —