Page 45 - 水利学报2021年第52卷第3期
P. 45
3
3
3
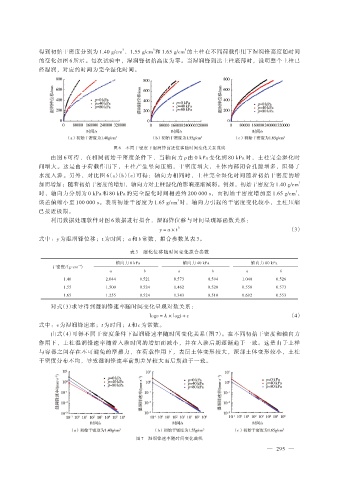
得到初始干密度分别为 1.40 g/cm 、1.55 g/cm 和 1.65 g/cm 的土柱在不同荷载作用下湿润锋高度随时间
的变化如图 6 所示。每次试验中,湿润锋初始高度为零。当湿润锋到达土柱底部时,说明整个土柱已
经湿润,对应的时间为完全湿化时间。
图 6 不同干密度下湿润锋前进位移随时间变化关系曲线
由图 6 可得,在相同初始干密度条件下,当轴向力 p 由 0 kPa 变化到 80 kPa 时,土柱完全湿化时
间增大。这是由于荷载作用下,土柱产生竖向压缩,干密度增大,土体内部闭合孔隙增多,阻碍了
水流入渗。另外,对比图 6(a)(b)(c)可得:轴向力相同时,土柱完全湿化时间随着初始干密度的增
3
加而增加;随着初始干密度的增加,轴向力对土柱湿化的影响逐渐减弱。例如,初始干密度为 1.40 g/cm
时,轴向力分别为 0 kPa 和 80 kPa 的完全湿化时间相差约 200 000 s,而初始干密度增加至 1.65 g/cm ,
3
该差值缩小至 100 000 s。表明初始干密度为 1.65 g/cm 时,轴向力引起的干密度变化较小,土柱压缩
3
已接近极限。
利用数据处理软件对图 6 数据进行拟合,湿润锋位移与时间呈现幂函数关系:
y = a × t b (3)
式中:y 为湿润锋位移;t 为时间;a 和 b 常数,拟合参数见表 3。
表 3 湿化位移随时间变化拟合参数
轴向力 0 kPa 轴向力 40 kPa 轴向力 80 kPa
干密度/(g·cm )
-3
a b a b a b
1.40 2.044 0.521 0.573 0.594 1.040 0.526
1.55 1.500 0.524 1.462 0.520 0.558 0.573
1.65 1.255 0.524 1.343 0.510 0.692 0.553
对式(3)求导得到湿润锋速率随时间变化呈现对数关系:
logv = λ × logt + c (4)
式中:v 为湿润锋速率;t 为时间;λ和 c 为常数。
由式(4)可得不同干密度条件下湿润锋速率随时间变化关系(图 7)。在不同初始干密度和轴向力
作用下,土柱湿润锋速率随着入渗时间的增加而减小,并在入渗后期逐渐趋于一致。这是由于土样
与容器之间存在不可避免的摩擦力,在荷载作用下,表层土体变形较大,深部土体变形较小,土柱
干密度分布不均,导致湿润锋速率前期差异较大而后期趋于一致。
图 7 湿润锋速率随时间变化曲线
— 295 —