Page 52 - 水利学报2021年第52卷第3期

5.0
4.5
4.0
） 3.5 卫星数据
（H 2O） 3.0

kg -1 2.5
（c）
（g 2.0
WUE/ 1.5
1.0
0.5
0.0
ENF EBF DBF MF CSH OSH SAV WSA Grass Crop Wetland
植被类型
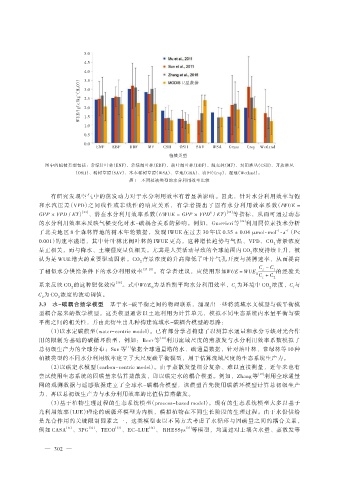
图中的植被类型包括：常绿针叶林（ENF）、常绿阔叶林（EBF）、落叶阔叶林（DBF）、混交林（MF）、封闭灌丛（CSH）、开放灌丛
（OSH）、稀树草原（SAV）、木本稀树草原（WSA）、草地（GRA）、农田（Crop）、湿地（Wetland）。
图 1 不同植被类型的水分利用效率比较

有研究发现空气中的蒸发动力对于水分利用效率有着显著影响。因此，针对水分利用效率与饱
和水汽压差（VPD）之间线性或非线性的响应关系，有学者提出了固有水分利用效率系数（IWUE =
［24］
［25］
K
GPP × VPD / ET） 、潜在水分利用效率系数（UWUE = GPP × VPD / ET） 等指标，从而可通过动态
的水分利用效率来反映气候变化对水-碳耦合关系的影响。例如，Guerrieri 等 ［26］ 利用同位素技术分析
了北美地区 8 个森林样地的树木年轮数据，发现 IWUE 在过去 30 年以 0.35 ± 0.04 μmol·mol ·a （P<
-1
-1
0.001）的速率递增，其中针叶林比阔叶林的 IWUE 更高，这种增长趋势与气温、VPD、CO 背景浓度
2
呈正相关，而与降水、土壤湿度呈负相关。尤其是人类活动导致的全球范围内 CO 浓度持续上升，被
2
认为是 WUE 增大的重要驱动因素。CO 背景浓度的升高降低了叶片气孔开度与蒸腾速率，从而提高
2
C - C
了相似水分供给条件下的水分利用效率 ［27-28］ 。有学者建议，应使用形如WUE = WUE i 1 的经验关
0 C + C 2
i
系来反映 CO 的这种肥化效应 ［29］ 。式中WUE 为基准期平均水分利用效率，C 为环境中 CO 浓度，C 与
2 0 i 2 1
C 为 CO 浓度的波动阈值。
2 2
3.3 水-碳耦合数学模型 基于水-碳平衡之间的物理联系，涌现出一些将流域水文模型与碳平衡模
型耦合起来的数学模型。这类模型通常以土地利用为计算单元，模拟不同生态系统内水量平衡与碳
平衡之间的相关性，并由此衍生出几种构建流域水-碳耦合模型的思路：
（1）以水定碳模型（water-centric model）。已有部分学者构建了以测算水通量和水分亏缺对光合作
用的限制为基础的碳循环模型，例如：Beer 等 ［30］ 利用流域尺度的蒸散发与水分利用效率系数模拟了
［1］
总初级生产力的全球分布；Sun 等 依据全球通量塔的水、碳通量数据，针对落叶林、常绿林等 10 种
植被类型的不同水分利用效率建立了大尺度碳平衡模型，用于估算流域尺度的生态系统生产力。
（2）以碳定水模型（carbon-centric model）。由于蒸散发量组分复杂、难以直接测量，近年来也有
尝试使用生态系统的固碳量来估算蒸散发，即以碳定水的耦合模型。例如，Zhang 等 ［19］ 利用全球通量
网的观测数据与遥感数据建立了全球水-碳耦合模型，该模型首先使用碳循环模型计算总初级生产
力，再以总初级生产力与水分利用效率的比值估算蒸散发。
（3）基于植物生理过程的生态系统模型（process-based model）。现有的生态系统模型大多以基于
光利用效率（LUE）理论的碳循环模型为内核，模拟植物在不同生长阶段的生理过程。由于水份供给
是光合作用的关键限制因素之一，这类模型也以不同方式考虑了水循环与固碳量之间的耦合关系，
［31］ ［32］ ［33］ ［34］ ［35］
例如 CASA 、3PG 、TECO 、EC-LUE 、 RHESSys 等模型，均通过对土壤含水量、蒸散发等

— 302 —