Page 19 - 2024年第55卷第12期

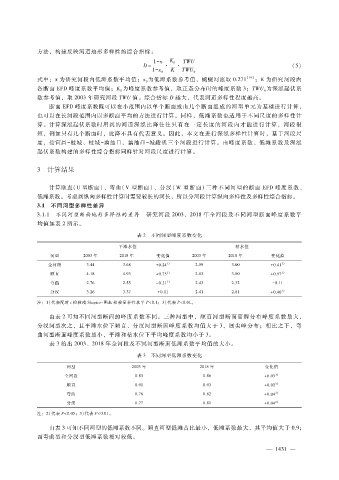
方法，构建反映河道地形多样性的综合指标：
ｘ Ｋ
１ － 珋 ０ ＴＷＵ
Ｄ ＝ · · （５）
１ － ｘ Ｋ ＴＷＵ
０ ０
ｘ为研究河段内低滩系数平均值；ｘ为低滩系数参考值，蜿蜒河流取 ０．２７１
式中： 珋 ［１６］ ；Ｋ为研究河段内
０
各断面 ＥＦＤ峰度系数平均值；Ｋ为峰度系数参考值，取正态分布时的峰度系数 ３；ＴＷＵ为深泓起伏系
０ ０
数参考值，取 ２００３年研究河段 ＴＷＵ值。综合指标 Ｄ越大，代表河道多样性程度越高。
断面 ＥＦＤ峰度系数既可以在小范围内以单个断面或由几个断面组成的河型单元为基础进行计算，
也可以在长河段范围内以多断面平均的方法进行计算。同样，低滩系数也适用于不同尺度的多样性计
算。计算深泓起伏系数时用到的河道深泓比降往往只有在一定长度的河段内才能进行计算，河段很
短，例如只有几个断面时，比降不具有代表意义。因此，本文在进行深泓多样性计算时，基于河段尺
度，按宜昌－ 枝城、枝城－ 藕池口、藕池口－ 城陵矶三个河段进行计算。由峰度系数、低滩系数及深泓
起伏系数构建的多样性综合指标同样针对河段尺度进行计算。

３ 计算结果

计算顺直（Ｕ型断面）、弯曲（Ｖ型断面）、分汊（Ｗ 型断面）三种不同河型的断面 ＥＦＤ峰度系数、
低滩系数。考虑到纵向多样性计算时需要较长的河长，所以分河段计算纵向多样性及多样性综合指标。
３．１ 不同河型多样性差异
３．１．１ 不同河型断面地形多样性的差异 研究河段 ２００３、２０１８年全河段及不同河型断面峰度系数平
均值如表 ２所示。

表 ２ 不同河型峰度系数变化

平滩水位 枯水位
河型 ２００３年 ２０１８年 变化值 ２００３年 ２０１８年 变化值
全河段 ３．４４ ３．６８ ＋ ０．２４ １） ２．５９ ３．００ ＋ ０．４１ ３）
顺直 ４．１８ ４．９３ ＋ ０．７５ ３） ２．８３ ３．８０ ＋ ０．９７ ３）
弯曲 ２．７６ ２．５５ － ０．２１ １） ２．４３ ２．３２ － ０．１１
分汊 ３．２６ ３．３７ ＋ ０．１１ ２．４１ ２．８１ ＋ ０．４０ １）
注：１）代表配对 ｔ检验或 Ｓｈａｐｉｒｏ － Ｗｉｌｋ检验显著性水平 Ｐ＜０．１；３）代表 Ｐ＜０．０１。

由表 ２可知不同河型断面的峰度系数不同。三种河型中，顺直河型断面高程分布峰度系数最大，
分汊河型次之，且平滩水位下顺直、分汊河型断面峰度系数均值大于 ３，属尖峰分布；相比之下，弯
曲河型断面峰度系数最小，平滩和枯水位下平均峰度系数均小于 ３。
表 ３给出 ２００３、２０１８年全河段及不同河型断面低滩系数平均值的大小。

表 ３ 不同河型低滩系数变化
河型 ２００３年 ２０１８年 变化值
全河段 ０．８３ ０．８６ ＋ ０．０３ ３）
顺直 ０．９１ ０．９３ ＋ ０．０２ ３）
弯曲 ０．７８ ０．８２ ＋ ０．０４ ３）
分汊 ０．７７ ０．８１ ＋ ０．０４ ２）
注：２）代表 Ｐ＜０．０５；３）代表 Ｐ＜０．０１。

由表 ３可知不同河型的低滩系数不同。顺直河型低滩占比最小，低滩系数最大，其平均值大于 ０．９；
而弯曲型和分汊型低滩系数相对较低。

４
— １ ３ １ —