Page 113 - 水利学报2021年第52卷第4期

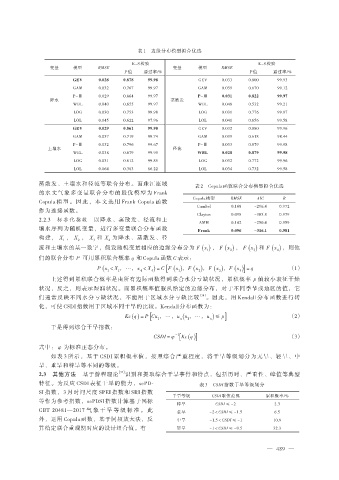
表 1 边缘分布模型拟合优选

K-S 检验 K-S 检验
变量 模型 RMSE 变量 模型 RMSE
P 值 通过率/% P 值 通过率/%
GEV 0.028 0.878 99.98 GEV 0.033 0.800 99.93
GAM 0.032 0.767 99.97 GAM 0.039 0.670 99.12
P-Ⅲ 0.029 0.864 99.97 P-Ⅲ 0.031 0.822 99.97
降水 蒸散发
WBL 0.040 0.655 99.97 WBL 0.048 0.532 99.21
LOG 0.030 0.753 99.98 LOG 0.031 0.776 99.97
LOL 0.045 0.622 97.96 LOL 0.041 0.656 99.58
GEV 0.029 0.861 99.98 GEV 0.032 0.880 99.96

GAM 0.037 0.719 99.74 GAM 0.039 0.618 98.44
P-Ⅲ 0.032 0.796 99.67 P-Ⅲ 0.033 0.879 99.98
土壤水 径流
WBL 0.038 0.679 99.95 WBL 0.028 0.879 99.98
LOG 0.031 0.612 99.85 LOG 0.032 0.772 99.96
LOL 0.064 0.383 86.22 LOL 0.034 0.732 99.58

蒸散发、土壤水和径流等联合分布。而珠江流域
表 2 Copula 函数联合分布模型拟合优选
的水文气象多变量联合分布的最优模型为 Frank
Copula 模型 RMSE AIC R
Copula 模 型 。 因 此 ， 本 文 选 用 Frank Copula 函 数
Gumbel 0.108 -296.4 0.972
作为连接函数。
Clayton 0.098 -305.8 0.979
2.2.3 标准化指数 以降水、蒸散发、径流和土
AMH 0.142 -250.4 0.959
壤水序列为随机变量，进行多变量联合分布函数 Frank 0.096 -316.1 0.981
构建， X ， X ， X 和 X 为降水、蒸散发、径
4
3
2
1
x
x
x
x
流和土壤水的某一数字，假设随机变量相应的边缘分布分为 F ( ) ， F ( ) ， F ( ) 和 F ( ) ，则他
1 2 3 4
们的联合分布 P 可用累积联合概率 q 和 Copula 函数 C 表示：
]
x
x
x
x
P (x < X ，，x < X ) = C [ F ( )，F ( )，F ( )，F ( ) = q （1）
1 1 4 4 1 2 2 4
上述得到累积联合概率是由所有边际函数得到联合水分亏缺状况，累积概率 p 值较小表征干燥
状况，反之，则表示湿润状况。而累积概率值服从给定的边缘分布，对于不同季节或地区的值，它
们通常反映不同水分亏缺状况，不能用于区域水分亏缺比较 ［38］ 。因此，用 Kendall 分布函数进行转
化，可使 CSDI 指数用于区域不同干旱的比较。Kendall 分布函数为：
)
Kc ( ) q = P [ Cu ，，u (u ，，u ≤ p ] （2）
1 n 1 n
于是得到综合干旱指数：
CSDI = φ [Kc ( ) q ] （3）
-1
式中： φ 为标准正态分布。
如表 3 所示，基于 CSDI 累积概率值，按照综合严重程度，将干旱等级划分为无旱、轻旱、中
旱、重旱和特旱等不同的等级。
2.3 其他方法 基于游程理论 ［37］ 识别和提取综合干旱事件和特点，包括历时、严重性、峰值等典型
特征。为反应 CSDI 表征干旱的能力，scPD⁃ 表 3 CSDI 指数干旱等级划分
SI 指数，3 月时间尺度 SPEI 指数和 SRI 指数
干旱等级 CSDI 取值范围 累积概率/%
等作为参考指数，scPDSI 指数计算基于国标
特旱 CSDI ≤ -2 2.3
GBT 20481—2017 气 象 干 旱 等 级 标 准 。 此 重旱 -2 < CSDI ≤ -1.5 6.5
外，运用 Copula 函数，基于同频放大法，反 中旱 -1.5 < CSDI ≤ -1 10.9
算给定联合重现期对应的设计组合值。有 轻旱 -1 < CSDI ≤ -0.5 32.3

— 489 —