Page 87 - 2021年第52卷第9期

录湿润锋变化，拍照时间按照先密后疏原则，并记录相应时刻马氏瓶内液面高度以计算入渗量。入
渗时间设为 75 h，入渗结束采用 TDR 测量土壤含水率。为减小试验误差，设置 3 个重复，试验结果取
重复的平均值。采用 Photoshop CS5 软件对所拍湿润锋图片进行裁剪，截取试样区域（40 cm×43 cm），
所对应的图像分辨率设置为 1600 像素×1720 像素。由于试样湿润区和干燥区具有较高对比度，故直
接选用魔棒工具分割湿润区和干燥区，分别使用黑白颜色填充，将其转化为黑白二值图像。最后利
用 Matlab R2016 软件编程对二值图像进行计算，得到湿润锋数据。

2.1.3 微润管出水特性试验 为研究微润管的出水性能，进行了不同压力水头下微润管空气出流试
验。将微润管置于空气中，通过橡皮软管与马氏瓶连接，调节马氏瓶高度给微润管提供不同压力水
头，记录各水头下微润管出流量随时间的变化。由试验数据发现，微润管单位时间出流量与压力水
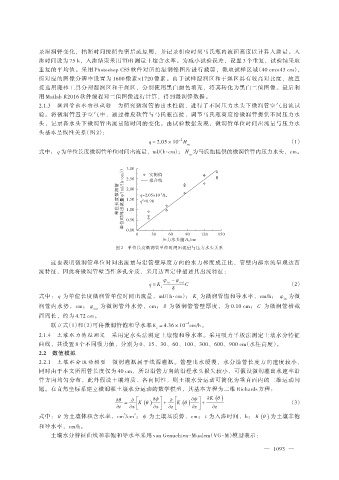
头基本呈线性关系（图 2）：
q = 2.05 × 10 H m （1）
-2
式中： q 为单位长度微润管单位时间出流量，ml/（h·cm）； H 为马氏瓶提供的微润管管内压力水头，cm。
m

） 3.00
（h · cm） 2.50 实测值
拟合线
单位长度微润管 单位时间出流量 q/ （ml/ 2.00 q=2.05×10 H m
-2
1.50
2
q =0.98
1.00
0.50
0.00
0 30 60 90 120 150
压力水头脑 H m/cm
图 2 单位长度微润管单位时间出流量与压力水头关系

这也表明微润管单位时间出流量与沿管壁厚度方向的水力梯度成正比，管壁内部水流呈现达西
流特征，因此将微润管壁当作多孔介质，采用达西定律描述其出流特征：
φ - φ
q = K in out C （2）
s δ
式中： q 为单位长度微润管单位时间出流量，ml/（h·cm）； K 为微润管饱和导水率，cm/h； φ 为微
s in
润管内水势，cm； φ 为微润管外水势，cm； δ 为微润管管壁厚度，为 0.10 cm； C 为微润管横截
out
面周长，约为 4.72 cm。
联立式（1）和（2）可得微润管饱和导水率K = 4.36 × 10 cm/h。
-4
s
2.1.4 土壤水力特征测定 采用定水头法测定土壤饱和导水率。采用吸力平板法测定土壤水分特征
曲线，共设置 8 个不同吸力值，分别为 0、15、30、60、100、300、600、900 cm（水柱高度）。
2.2 数值模拟

2.2.1 土壤水分运动模型 微润灌溉属于线源灌溉。管壁出水缓慢，水分沿管长度方向速度较小，
同时由于本文所用管长度仅为 40 cm，所以沿管方向的沿程水头损失较小，可假设微润灌出水速率沿
管方向均匀分布，此外假设土壤均质、各向同性，则土壤水分运动可简化为垂直面内的二维运动问
题。在直角坐标系建立微润灌土壤水分运动的数学模型，其基本方程为二维 Richards 方程：
θ
∂θ = ∂ é êK ( ) ∂ψ ù ú + ∂ é êK ( ) ∂ψ ù ú + ∂K ( ) （3）
θ
θ
∂t ∂x ë ∂x û ∂z ë ∂z û ∂z
θ
式中： θ 为土壤体积含水率，cm /cm ； ψ 为土壤基质势，cm； t 为入渗时间，h； K ( ) 为土壤非饱
3
3
和导水率，cm/h。
土壤水分特征曲线和非饱和导水率采用 van Genuchten-Mualem（VG-M）模型表示：
— 1093 —