Page 33 - 水利学报2021年第52卷第11期

60 60
（kN · m） 40 40

弯距/ 20 20 剪力/kN

0 0

-20 -20
0 2 4 6 8 10
x/m
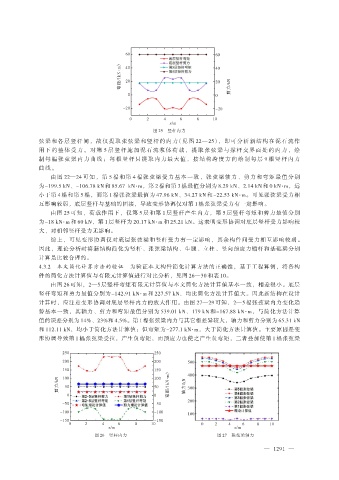
图 25 竖杆内力
弦 梁 和 各 层 竖 杆 间 ， 故 仅 提 取 张 弦 梁 和 竖 杆 的 内 力（见 图 22—25）， 即 可 分 析 新 结 构 在 泥 石 流 作
用 下 的 整 体 受 力 。 对 第 5 层 竖 杆 施 加 泥 石 流 浆 体 荷 载 ， 提 取 张 弦 梁 与 撑 杆 交 界 面 处 的 内 力 ， 绘
制 每 榀 张 弦 梁 内 力 曲 线 ； 每 根 竖 杆 只 提 取 内 力 最 大 值 ， 按 结 构 跨 度 方 向 绘 制 每 层 9 根 竖 杆 内 力
曲线。
由图 22—24 可知，第 5 榀和第 4 榀张弦梁受力基本一致，张弦梁轴力、剪力和弯矩最值分别
为-199.5 kN、-106.78 kN 和 85.67 kN·m，第 2 榀和第 3 榀最值分别为 8.29 kN、2.14 kN 和 0 kN·m，远
小于第 4 榀和第 5 榀，而第 1 榀张弦梁最值为 47.96 kN、34.27 kN 和-22.53 kN·m。可见张弦梁受力相
互影响较弱，底层竖杆与基础的固接，导致变形协调仅对第 1 榀张弦梁受力有一定影响。
由图 25 可知，荷载作用下，仅第 5 层和第 1 层竖杆产生内力，第 5 层竖杆弯矩和剪力最值分别
为-18 kN·m 和 60 kN，第 1 层竖杆为 20.17 kN·m 和 25.21 kN。这表明变形协调对底层竖杆受力影响较
大，对相邻竖杆受力无影响。
综上，可见变形协调仅对底层张弦梁和竖杆受力有一定影响，其余构件间受力相互影响较弱。
因此，理论分析时将新结构简化为竖杆、张弦梁结构、牛腿、立柱、竖向预应力锚杆和基础梁分别
计算是比较合理的。
4.3.2 本文简化计算方法的验证 为验证本文构件简化计算方法的正确性，基于工程算例，将各构
件的简化方法计算值与有限元计算值进行对比分析，见图 26—30 和表 10。
由图 26 可知，2—5 层竖杆弯矩有限元计算值与本文简化方法计算值基本一致，相差很小。底层
竖杆弯矩和剪力最值分别为-142.91 kN·m 和 227.57 kN，均比简化方法计算值大。因此新结构在设计
计算时，应注意变形协调对底层竖杆内力的放大作用。由图 27—29 可知，2—5 榀张弦梁内力变化趋
势基本一致，其轴力、剪力和弯矩最值分别为 539.01 kN、179 kN 和-167.88 kN·m，与简化方法计算
值的误差分别为 14%、23%和 4.5%。第 1 榀张弦梁内力与其它榀差异较大，轴力和剪力分别为 65.31 kN
和 112.11 kN，均小于简化方法计算值；但弯矩为-277.1 kN·m，大于简化方法计算值。主要原因是变
形协调导致第 1 榀张弦梁受拉，产生负弯矩，而预应力也使之产生负弯矩，二者叠加使第 1 榀张弦梁

250 250
200 200 500
150 150 400
剪力/kN 100 100 （kN · m） 轴力/kN 300
50
50
0 0 弯距/
200
-50 -50
-100 -100
100
-150 -150
0 2 4 6 8 10 0 2 4 6 8 10
x/m x/m
图 26 竖杆内力 图 27 张弦梁轴力

— 1291 —