Page 33 - 2022年第53卷第4期
P. 33
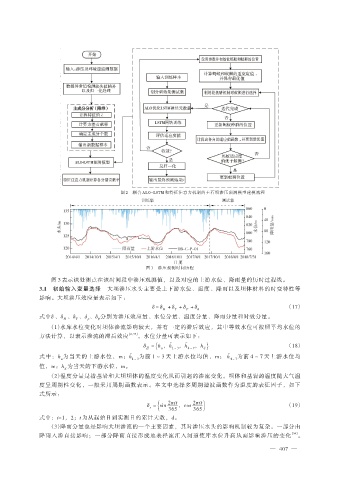
图 2 耦合 ALO-LSTM 和特征注意力机制的土石坝渗压预测模型建模流程
日期
图 3 渗压观测时间历程
图 3 表示该处测点在该时间段中渗压观测值,以及对应的上游水位、降雨量的历时过程线。
3.1 初始输入变量选择 大坝渗压水头主要受上下游水位、温度、降雨以及坝体材料的时变特性等
影响。大坝渗压效应量表示如下:
δ = δ + δ + δ + δ θ (17)
H
P
T
式中δ 、δ 、δ 、δ 、δ 分别为渗压效应量、水位分量、温度分量、降雨分量和时效分量。
θ
H
T
p
(1)水库水位变化对坝体渗流影响较大,并有一定的滞后效应,其中等效水位可按照平均水位的
方法计算,以表示渗流的滞后效应 [2,33] 。水位分量可表示如下:
δ ={h ,h ˉ 1 - 3 ,h ˉ 4 - 7 ,h d } (18)
u
H
式中:h 为当天的上游水位,m;h ˉ 为前 1 ~ 3 天上游水位均值,m; h ˉ 为前 4 ~ 7 天上游水位均
u 1 - 3 4 - 7
值,m;h 为当天的下游水位,m。
d
(2)温度分量是指基岩和大坝坝体的温度变化从而引起的渗流变化。坝体和基岩的温度随大气温
度呈周期性变化,一般采用周期函数表示。本文中选择多周期谐波函数作为温度的表征因子,如下
式所示:
r { 2πit 2πit }
δ = sin 365 ,cos 365 (19)
式中:i=1,2;t为从起始日到实测日的累计天数,d。
(3)降雨分量也是影响大坝渗流的一个主要因素,其对渗压水头的影响机制较为复杂。一部分由
降雨入渗直接影响;一部分降雨直接形成地表径流汇入河道使库水位升高从而影响渗压的变化 [34] 。
— 407 —