Page 31 - 2022年第53卷第8期
P. 31
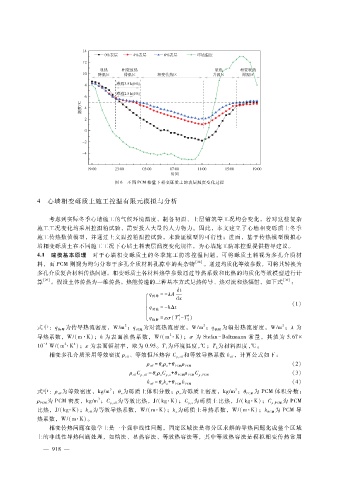
图 6 不同 PCM掺量下相变砾质土的表层温度变化过程
4 心墙相变砾质土施工控温有限元模拟与分析
考虑到实际冬季心墙施工的气候环境温度、制备初温、上层铺筑等工况均会变化,若对这些复杂
施工工况变化均采用控温箱试验,需要投入大量的人力物力。因此,本文建立了心墙相变砾质土冬季
施工传热数值模型,并通过上文温控箱温控试验,来验证模型的可行性;进而,基于传热模型模拟心
墙相变砾质土在不同施工工况下心墙土料表层温度变化规律,为心墙施工防冻控温提供指导建议。
4.1 建模基本原理 对于心墙相变砾质土的冬季施工防冻控温问题,可将砾质土料视为多孔介质材
料,而 PCM则视为均匀分布于多孔介质材料孔隙中的夹杂物 [28] 。通过均质化等效参数,可将其转换为
多孔介质复合材料传热问题。相变砾质土各材料热学参数通过导热系数和比热的均质化等效模型进行计
算 [29] 。假设土体传热为一维传热。热能传递的三种基本方式是热传导、热对流和热辐射,如下式 [30] :
dt
q =- λ A
传导
dx
( 1)
q =- h Δ t
对流
4
4
q = εσ (T- T)
2
辐射
1
2
2
2
式中:q 为传导热流密度,W?m ;q 为对流热流密度,W?m ;q 为辐射热流密度,W?m ;λ为
传导
辐射
对流
2
导热系数,W?(m·K);h为表面换热系数,W?(m·K);σ为 Stefan - Boltzmann常量,其值为 5.67 ×
- 8
2
4
10 W?(m·K);ε 为表面辐射率,取为 0.95。T为环境温度,℃;T为材料温度,℃。
1 2
、等效恒压热容 C 和等效导热系数 k ,计算公式如下:
相变多孔介质采用等效密度 ρ eff
p,eff eff
= + (2)
ρ eff θ s ρ s θ PCM ρ PCM
C = C + C (3)
ρ eff p,eff θ s ρ s p,s θ PCM ρ PCM p,PCM
k+ k (4)
eff
k = θ s s θ PCM PCM
3 3
式中:ρ eff 为等效密度,kg?m ;θ s 为砾质土体积分数;ρ s 为砾质土密度,kg?m ;θ PCM 为 PCM体积分数;
3
为 PCM密度,kg?m ;C 为等效比热,J?(kg·K);C 为砾质土比热,J?(kg·K);C 为 PCM
ρ PCM p,eff p,s p,PCM
比热,J?(kg·K);k 为等效导热系数,W?(m·K);k为砾质土导热系数,W?(m·K);k 为 PCM 导
PCM
eff
s
热系数,W?(m·K)。
相变传热问题在数学上是一个强非线性问题,固定区域法是将分区求解的导热问题化成整个区域
上的非线性导热问题处理,如焓法、显热容法、等效热容法等,其中等效热容法是模拟相变传热常用
8
— 9 1 —