Page 79 - 2024年第55卷第8期

 Ｔ
Ｃ ｄｔｄｘｄｙｄｚ （４）
Ｑ ＝ ρ ｅ ｐ，ｅ
Ｔ
 ｔ
和 Ｃ 分别为相变黏土的等效导热系数、
式中：ｋ、ρ ｅ ｐ，ｅ
ｅ
密度和比热； Ｔ?  ｚ为 ｚ方向的温度梯度； Ｔ?  ｔ为微
单元体的变温速率；Ｔ为温度场；ｔ为传热时间。
依据热量平衡原理，可对心墙相变黏土建立如下
热量平衡方程：
Ｑ － Ｑ＋ Ｑ ＝ Ｑ （５）
ｚ ＋ ｄｚ ｚ ｏｕｔ Ｔ
 Ｔ
２
Ｃ
ｅ ｃ ａ ｓ
ｋ Ｔ ＋ ｑ＋ ｑ－ ｑ＝ ρ ｅ ｐ，ｅ （６）
Δ
 ｔ
２．３ 热学参数均质化等效模型 基于复合材料的等效
热学参数的经验与理论方法，建立了适用于松铺土料
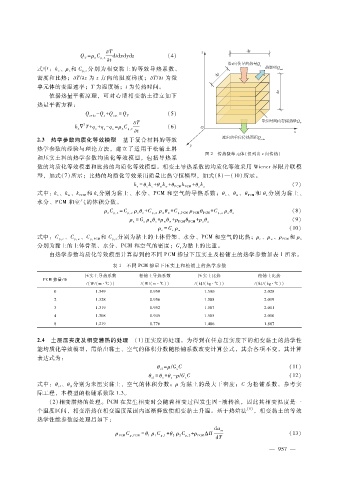
图 ２ 传热微单元体（仅列出 ｚ向传热）
和压实土料的热学参数均质化等效模型，包括导热系
数的均质化等效模型和比热的均质化等效模型。相变土导热系数的均质化等效采用 Ｗｉｅｎｅｒ界限并联模
型，如式（７）所示；比热的均质化等效采用质量比热守恒模型，如式（８）—（１０）所示。
ｋ＋ ｋ＋ ｋ ＋ ｋ （７）
ｅ
ｋ＝ θ ｃ ｃ θ ｗ ｗ θ ＰＣＭ ＰＣＭ θ ａ ａ
、 分别为黏土、
式中：ｋ、ｋ、ｋ 和 ｋ分别为黏土、水分、ＰＣＭ 和空气的导热系数；θ ｃ θ ｗ 、θ ＰＣＭ 和 θ ａ
ｃ ｗ ＰＣＭ ａ
水分、ＰＣＭ和空气的体积分数。
＋ Ｃ ＋ Ｃ （８）
ｐ，ａ
Ｃ ＝ Ｃ ρ ｃ θ ｃ
ρ ｅ ｐ，ｅ ｐ，ｃ ｐ，ｗ ρ ｗ θ ｗ ｐ，ＰＣＭ ρ ＰＣＭ θ ＰＣＭ ＋ Ｃ ρ ａ θ ａ
＋ ＋ ＋ （９）
ｓ
ρ ｅ ＝ Ｇ ρ ｗ θ ｃ ρ ｗ θ ｗ ρ ＰＣＭ θ ＰＣＭ ρ ａ θ ａ
（１０）
ｓ
ρ ｃ ＝ Ｇ ρ ｗ
、
式中：Ｃ 、Ｃ 、Ｃ 和 Ｃ 分别为黏土的土体骨架、水分、ＰＣＭ和空气的比热；ρ ｃ ρ ｗ 、ρ ＰＣＭ 和 ρ ａ
ｐ，ｃ ｐ，ｗ ｐ，ＰＣＭ ｐ，ａ
分别为黏土的土体骨架、水分、ＰＣＭ和空气的密度；Ｇ为黏土的比重。
ｓ
由热学参数均质化等效模型计算得到的不同 ＰＣＭ掺量下压实土及松铺土的热学参数如表 １所示。
表 １ 不同 ＰＣＭ掺量下压实土和松铺土的热学参数
压实土导热系数 松铺土导热系数 压实土比热 松铺土比热
ＰＣＭ掺量?％
?（Ｗ?（ｍ·℃）） ?（Ｗ?（ｍ·℃）） ?（ｋＪ?（ｋｇ·℃）） ?（ｋＪ?（ｋｇ·℃））
０ １．３４９ ０．９５９ １．５９０ ２．０２８
２ １．３２８ ０．９５６ １．５８８ ２．０１９
３ １．３１９ ０．９５２ １．５８７ ２．０１１
４ １．３０８ ０．９４５ １．５８５ ２．０１０
８ １．２１９ ０．７７６ １．４８６ １．８８７

２．４ 土层压实度及相变潜热的处理 （１）压实度的处理。为得到在任意压实度下的相变黏土的热学性
能均质化等效模型，需给出黏土、空气的体积分数随松铺系数改变计算公式，其余各项不变，其计算
表达式为：
＝
θ ｃｌ ρ ?ＧＣ （１１）
ｓ
θ ａｌ θ ｃ θ ａ ρ ?ＧＣ （１２）
＝ ＋ －
ｓ
分别为未压实黏土、空气的体积分数；ρ 为黏土的最大干密度；Ｃ为松铺系数，参考实
式中：θ ｃｌ 、θ ａｌ
际工程，本模型的松铺系数取 １．３。
（ ２）相变潜热的处理。ＰＣＭ在发生相变时会随着相变过程发生固 － 液转换，因此其相变温度是一
个温度区间，相变潜热在相变温度范围内逐渐释放使相变黏土升温。基于热焓法 ［８］ ，相变黏土的等效
热学性能参数经处理后如下：
ｄａ ｍ
Ｃ ＝ Ｃ ＋ ρ ＰＣＭ Δ Ｈ （１３）
ρ ＰＣＭ ｐ，ＰＣＭ θ １ ρ １ Ｃ ＋ θ ２ ρ ２ ｐ，２
ｐ，１
ｄＴ
— ９ ５ ７ —