Page 134 - 2024年第55卷第11期

帷幕的达到控制指标的时间标准差为 ６．４１ａ，比其他坝基防渗体达到控制指标的时间标准差大，表明
副防渗帷幕达到控制指标的时间受水泥基材料参数空间变异性影响较大；仅考虑防渗结构下服役年限
均值为 ７９．３ａ，考虑防渗与受力结构下服役年限均值为 ７２．２ａ。
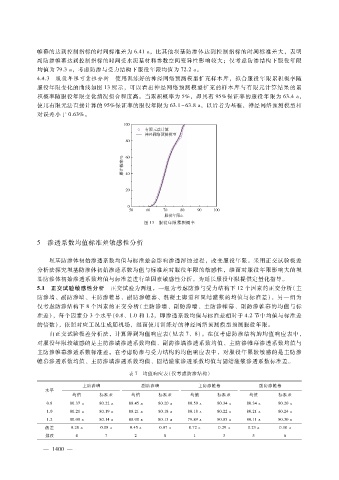
４．４．３ 服役年限可靠性分析 使用训练好的神经网络预测模型扩充样本库，拟合服役年限累积概率随
服役年限变化的曲线如图 １３所示，可以看出神经网络预测模型扩充的样本库与有限元计算结果的累
积概率随服役年限变化情况拟合程度高。当累积概率为 ５％，即具有 ９５％保证率的服役年限为 ６３．４ａ，
使用有限元法直接计算的 ９５％保证率的服役年限为 ６３．１～６３．８ａ，以后者为基准，神经网络预测模型相
对误差小于 ０．６３％。

图 １３ 服役年限累积概率

５ 渗透系数均值标准差敏感性分析

坝基防渗体初始渗透系数均值与标准差会影响渗透溶蚀过程，改变服役年限。采用正交试验极差
分析法探究坝基防渗体初始渗透系数均值与标准差对服役年限的敏感性，继而对服役年限影响大的坝
基防渗体初始渗透系数均值与标准差进行单因素敏感性分析，为延长服役年限提供定量化指导。
５．１ 正交试验敏感性分析 正交试验为两组，一组为考虑防渗与受力结构下 １２个因素的正交分析（主
防渗墙、副防渗墙、主防渗帷幕、副防渗帷幕、混凝土廊道和固结灌浆的均值与标准差），另一组为
仅考虑防渗结构下 ８个因素的正交分析（主防渗墙、副防渗墙、主防渗帷幕、副防渗帷幕的均值与标
准差），每个因素分 ３个水平（０．８、１．０和 １．２，即渗透系数均值与标准差相对于 ４．２节中均值与标准差
的倍数），依照对应工况生成随机场，继而使用训练好的神经网络预测模型预测服役年限。
由正交试验极差分析法，计算得到均值响应表（见表 ７、８）。在仅考虑防渗结构的均值响应表中，
对服役年限较敏感的是主防渗墙渗透系数均值、副防渗墙渗透系数均值、主防渗帷幕渗透系数均值与
主防渗帷幕渗透系数标准差。在考虑防渗与受力结构的均值响应表中，对服役年限较敏感的是主防渗
帷幕渗透系数均值、主防渗墙渗透系数均值、固结灌浆渗透系数均值与固结灌浆渗透系数标准差。

表 ７ 均值响应表（仅考虑防渗结构）
主防渗墙 副防渗墙 主防渗帷幕 副防渗帷幕
水平
均值 标准差 均值 标准差 均值 标准差 均值 标准差
０．８ ８０．３７ａ ８０．２２ａ ８０．４５ａ ８０．２０ａ ８０．５９ａ ８０．３４ａ ８０．３４ａ ８０．２０ａ
１．０ ８０．２１ａ ８０．１９ａ ８０．２１ａ ８０．１８ａ ８０．１８ａ ８０．２２ａ ８０．２１ａ ８０．２４ａ
１．２ ８０．０８ａ ８０．１４ａ ８０．００ａ ８０．１３ａ ７９．８９ａ ８０．０５ａ ８０．１１ａ ８０．３０ａ
极差 ０．２８ａ ０．０８ａ ０．４５ａ ０．０７ａ ０．７２ａ ０．２９ａ ０．２３ａ ０．１０ａ
排秩 ４ ７ ２ ８ １ ３ ５ ６

— １ ４ ０ —
０