Page 130 - 2024年第55卷第11期

代次数设为 １０００次，不同超参数组合的最大贝叶斯优化次数 Ｎ为 ３０次，神经网络预测模型在验证集
上的 ＲＭＳＥ最大容差 ε 设为 １ａ。表 ４列出了超参数的优化区间，同时给出了超参数初始值与最优值。
表 ４ 超参数优化结果

超参数 优化区间 超参数初始值 超参数最优值
第一层 １０～１０００ ５００ 第一层 ８５７
隐藏层神经元个数 第二层 １０～１０００ ５００ 第二层 ２４４
第三层 １０～１０００ ２００ 第三层 ３７
－ ９
正则化强度 ［ １ × １０ ，２０］ １ ６．５０ × １０ － ５
－ ６
学习率 ［１ × １０ ，１］ １ × １０ － ３ ３．２２ × １０ － ５
图 ５为神经网络预测模型在验证集上的 ＲＭＳＥ与贝叶斯优化次数的关系，贝叶斯优化初期需要通
过计算超参数组合获得超参数的概率分布，因此前 ４次优化中，神经网络预测模型在验证集上观测到
的 ＲＭＳＥ并没有明显下降，随后神经网络预测模型在验证集上观测到的 ＲＭＳＥ逐步降低至小于 １ａ，且
观测到的 ＲＭＳＥ在第 １１次优化后达到稳定，表明超参数已优化至最优。神经网络预测模型在第 ４次至
１１次优化过程中的 ＲＭＳＥ与估计的 ＲＭＳＥ均持续降低并差距较小，均证明了贝叶斯优化的有效性。神
经网络预测模型在贝叶斯优化第 ３０次的训练集与验证集如图 ６所示，训练集与验证集上的拟合系数
２
Ｒ分别为 ０．９６４７与 ０．９５３５，证明了贝叶斯优化后神经网络预测模型的准确性。

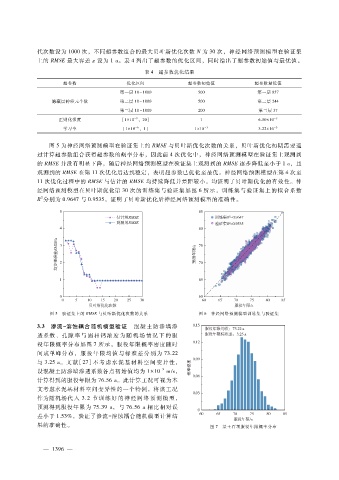
图 ５ 验证集上的 ＲＭＳＥ与贝叶斯优化次数的关系 图 ６ 神经网络预测模型训练集与验证集

３．３ 渗流－ 溶蚀耦合随机模型验证 混凝 土防渗墙 渗
透系数、孔 隙 率 与 固 相 钙 浓 度 为 随 机 场 情 况 下 的 服
役年限概率分布如图 ７所示，服役年限概率密度随时
间成单峰分布，服役年 限均 值与 标准 差分别为 ７３．２２
与 ３．２５ａ。文献 ［２７］不 考虑 水泥 基材 料空 间变异 性，
－ ９
设混凝土防渗墙渗透系数各点初始值均为 １ × １０ ｍ?ｓ，
计算得到的服役年限为 ７６．５６ａ。此计算工况可视为本
文考虑水泥基材料空间变异性的一个特例，将该工况
作为随机场 代 入 ３．２节 训 练 好 的 神 经 网 络 预 测 模 型，
预测得到服役年限为 ７５．３９ａ，与 ７６．５６ａ相比相对误
差小于 １．５３％，验证了渗流－ 溶蚀耦合随机模型计算结
果的准确性。 图 ７ 某土石坝服役年限概率分布

９
— １ ３ ６ —