Page 128 - 2024年第55卷第11期

水泥基材料中的扩散系数，Ｈ（ｘ）为单位跃迁函数，当 ｘ＜０时，Ｈ（ｘ） ＝０，否则 Ｈ（ｘ） ＝１；ｋ 为水泥基
０
材料的初始渗透系数随机场。
２．２ 贝叶斯优化的神经网络预测模型 本文以水泥基材料达到控制指标的时间为服役年限，水泥基材
料参数随机场作为输入变量，渗流－ 溶蚀耦合随机模型计算的服役年限为输出结果，使用神经网络建
立随机场与服役年限之间映射关系的预测模型。贝叶斯优化的神经网络预测模型理论框架如图 ２所
示，输入层为渗透系数 ｋ、固相钙浓度 Ｃ 和孔隙率 θ 初始值随机场，输出层即服役年限 Ｔ。采用贝叶
ｓ
［２５］
斯优化选择超参数 ｓ ，当神经网络预测模型在验证集上预测的服役年限均方根差 ＲＭＳＥ大于容差 ε
时，计算已知 ＲＭＳＥ条件下超参数的概率分布 η （ｓＲＭＳＥ），选择最小化 ＲＭＳＥ条件下的超参数，重新
训练神经网络预测模型。

图 ２ 贝叶斯优化的神经网络预测模型理论框架

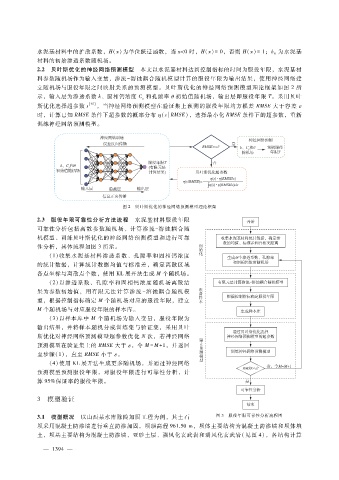
２．３ 服役年限可靠性分析方法流程 水泥基材料服役年限
可靠性分析包括离散参数随机场、计算渗流－ 溶蚀耦 合随
机模型、训练贝叶斯优化的神经网络预测模型和进行可靠
性分析，具体流程如图 ３所示。
（ １）收集水泥基材料渗透系数、孔隙率和固相钙浓度
的统计数据，计算统计数据均值与标准差，确定离散区域
各点坐标与离散点个数，使用 ＫＬ展开法生成 Ｍ个随机场。
（２）以渗透系数、孔隙率和固相钙浓度随机场离散结
果为参数初始值，用有限元法计算渗流 － 溶蚀耦合随机模
型，根据控制指标确定 Ｍ个随机场对应的服役年限，建立
Ｍ个随机场与对应服役年限的样本库。
（３）以样本库中 Ｍ 个随机场为输入变量，服役年限为
输出结果，并将样本随机分成训练集与验证集，采用贝叶
斯优化对神经网络预测模型超参数优化 Ｎ次，若神经网络
预测模型在验证集上的 ＲＭＳＥ大于 ε ，令 Ｍ＝ Ｍ＋ １，并返回
至步骤（１），直至 ＲＭＳＥ小于 ε 。
（４）使用 ＫＬ展开法生成更多随机场，并通过神经网络
预测模型预测服役年限，对服役年限进行可靠性分析，计
算 ９５％保证率的服役年限。

３ 模型验证

３．１ 模型概况 以山西某水库除险加固工程为例，其土石 图 ３ 服役年限可靠性分析流程图
坝采用混凝土防渗墙进行垂直防渗加固。坝顶高程 ９６１．５０ｍ，坝体主要结构为混凝土防渗墙和坝体填
土，坝基主要结构为混凝土防渗墙、亚砂土层、强风化玄武岩和弱风化玄武岩（见图 ４），各结构计算

９
— １ ３ ４ —