Page 48 - 2025年第56卷第10期

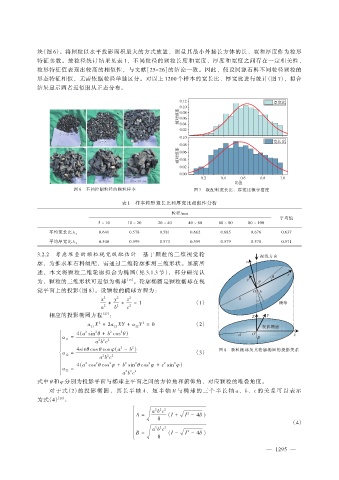
块（图 6）。将颗粒以水平投影面积最大的方式放置，测量其最小外接长方体的长、宽和厚度作为粒形
特征参数。按粒径统计结果见表 1，不同粒径的颗粒长度和宽度、厚度和宽度之间存在一定相关性，
粒形特征值表现出较高的相似性，与文献［25-26］的结论一致。因此，假设同源石料不同粒径颗粒的
形态特征相似，无需依据粒径单独区分。对以上 1200 个样本的宽长比、厚宽比进行统计（图 7），拟合
结果显示两者近似服从正态分布。

图 6 不同控制粒径的颗粒样本 图 7 级配料宽长比、厚宽比概率密度

表 1 样本粒形宽长比和厚宽比相似性分析
粒径/mm
平均值
5 ~ 10 10 ~ 20 20 ~ 40 40 ~ 60 60 ~ 80 80 ~ 100
0.641 0.578 0.581 0.662 0.685 0.676 0.637
平均宽长比 λ 1
0.540 0.599 0.573 0.559 0.579 0.578 0.571
平均厚宽比 λ 2
3.2.2 考虑堆叠的颗粒视觉级配估计 基于颗粒的二维视觉轮
廓，为推求堆石料级配，需通过二维轮廓推测三维形状。如前所
述，本文将颗粒二维轮廓拟合为椭圆（见 3.1.3 节），部分研究认
为，颗粒的三维形状可近似为椭球 ［13］ 。轮廓椭圆是颗粒椭球在视
觉平面上的投影（图 8）。设颗粒的椭球方程为：
x 2 y 2 z 2
+ + = 1 （1）
a 2 b 2 c 2
相应的投影椭圆方程 ［27］ ：

2
2
a 11 X + 2a 12 XY + a 22 Y = 0 （2）
ì 4(a sin θ + b cos θ )
2
2
2
2
ï
ïa 11 =
ï a b c 2
2
2
ï
ï ï 4sinθ cos θ cos φ (a - b ) 图 8 颗粒椭球及其轮廓椭圆的投影关系
2
2
í a 12 = （3）
ï ï a b c 2
2
2
ï
ï 4(a cos θ cos φ + b sin θ cos φ + c sin φ)
2
ï
2
2
2
2
2
2
2
ï ï a b c 2
ï a 22 =
î
2
2
式中 θ 和 φ 分别为投影平面与椭球主平面之间的方位角和俯仰角，对应颗粒的堆叠角度。
对 于 式（2）的 投 影 椭 圆 ， 其 长 半 轴 A、 短 半 轴 B 与 椭 球 的 三 个 半 长 轴 a、 b、 c 的 关 系 可 以 表 示
为式（4） ：
［28］
ì a b c 2
ï (I + I - 4δ )
2
2
2
ï A =
ï ï 8
í （4）
ï ï a b c 2
ï
2
2
2
ï ï
ï B = 8 (I - I - 4δ )
î
— 1295 —