Page 97 - 2025年第56卷第10期

域，使得 OTSU 阈值分割法失效（图 4），即使使用人工选择阈值仍很难将图像很好地进行二值化（图
12）。而通过维纳滤波处理该图像，则可使图像更锐化，锐化过的图像可让流凌边界更加清晰，也让
河水反光的部分更模糊，反光部分的平均亮度也变得更低，从而更好地区分河水部分以及流凌，使精
度变高（图 13）。

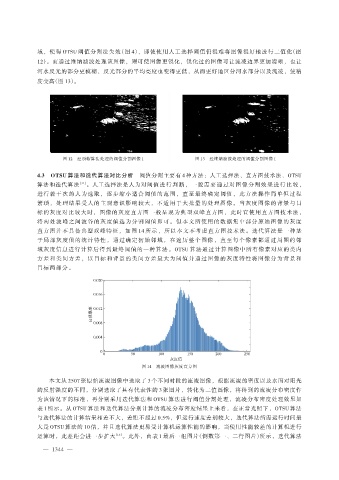
图 12 经顶帽算法处理的阈值分割图像 1 图 13 经维纳滤波处理的阈值分割图像 1

4.3 OTSU 算法和迭代算法对比分析 阈值分割主要有 4 种方法：人工选择法、直方图技术法、OTSU
算法和迭代算法 ［31］ 。人工选择法是人为对阈值进行判断，一般需要通过对图像分割效果进行比较，
进行若干次的人为选取，逐步缩小适合阈值的范围，直至最终确定阈值，此方法操作简单但过程
繁琐，处理结果受人的主观意识影响较大，不适用于大批量的处理图像。当灰度图像的背景与目
标的灰度对比较大时，图像的灰度直方图一般呈现为典型双峰直方图，此时宜使用直方图技术法，
将两处波峰之间波谷的灰度值选为分割阈值即可。但本文所使用的数据集中部分原始图像的灰度
直方图并不具备典型双峰特征，如图 14 所示，所以本文不考虑直方图技术法。迭代算法是一种基
于局部灰度值的统计特性，通过确定初始邻域，在遍历整个图像，直至每个像素都通过周围的邻
域灰度信息进行计算后得到最终阈值的一种算法。OTSU 算法通过计算图像中所有像素对应的类内
方差和类间方差，以目标和背景的类间方差最大为阈值并通过图像的灰度特性将图像分为背景和
目标两部分。

图 14 流凌图像灰度直方图

本文从 2507 张原始流凌图像中选取了 3 个不同时段的流凌图像，根据流凌的密度以及水面对阳光
的反射强度的不同，分别选取了具有代表性的 3 张图片，转化为二值图像，将得到的流凌分布密度作
为该情况下的标准，再分别采用迭代算法和 OTSU 算法进行阈值分割处理，流凌分布密度处理效果如
表 1 所示。从 OTSU 算法和迭代算法分别计算的流凌分布密度结果上来看，在正常光照下，OTSU 算法
与迭代算法的计算结果相差不大，差距不超过 0.5%，但运行速度差别较大，迭代算法所需运行时间最
大是 OTSU 算法的 10 倍，并且迭代算法更易受计算机运算性能的影响，当使用性能较差的计算机进行
运算时，此差距会进一步扩大 ［16］ 。此外，由表 1 最后一组图片（倒数第一、二行图片）所示，迭代算法

— 1344 —