Page 7 - 水利学报2021年第52卷第3期

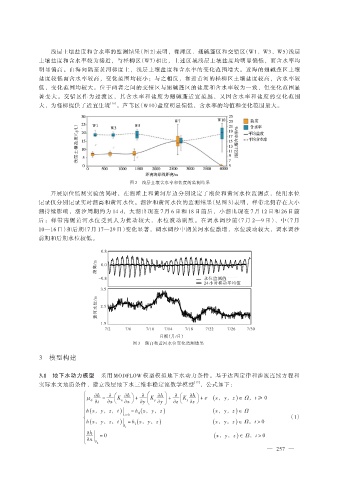
浅层土壤盐度和含水率的监测结果（图 2）表明，裸滩区、翅碱蓬区和交错区（W1、W3、W5）浅层
土壤盐度和含水率较为接近，与柽柳区（W7）相比，上述区域浅层土壤盐度均明显偏低，而含水率均
明显偏高。由海向陆至黄河梯度上，浅层土壤盐度和含水率的变化范围增大。近海的翅碱蓬区土壤
盐度较低而含水率较高，变化范围均较小；与之相反，靠近黄河的柽柳区土壤盐度较高，含水率较
低，变化范围均较大。位于两者之间的交错区与翅碱蓬区的盐度和含水率较为一致，但变化范围显
著变大。交错区作为过渡区，其含水率和盐度为翅碱蓬适宜范围，又因含水率和盐度的变化范围
大，为柽柳提供了适宜生境 ［16］ 。芦苇区（W10）盐度明显偏低，含水率的均值和变化范围最大。

（g/L）

浅层土壤盐度/

图 2 浅层土壤含水率和盐度的监测结果
开展原位监测实验的同时，在潮滩上和黄河岸边分别设定了潮位和黄河水位监测点，使用水位
记录仪分别记录实时潮高和黄河水位。潮汐和黄河水位的监测结果（见图 3）表明，样带北侧存在大小
潮持续影响，潮汐周期约为 14 d，大潮出现在 7 月 6 日和 18 日前后，小潮出现在 7 月 12 日和 26 日前
后；样带南侧黄河水位受到人为扰动较大，水位波动剧烈。在调水调沙前（7 月 2—9 日）、中（7 月
10—16 日）和后期（7 月 17—29 日）变化显著，调水调沙中期黄河水位激增，水位波动较大，调水调沙
前期和后期水位较低。

0.8
湖高/m 0.0

-0.8 水位监测值
24 小时移动平均值
3.5
黄河水位/m 2.5

1.5
7/2 7/6 7/10 7/14 7/18 7/22 7/26 7/30
日期（月/日）
图 3 潮高和黄河水位变化监测结果

3 模型构建

3.1 地下水动力模型 采用 MODFLOW 模型模拟地下水动力条件。基于达西定律和渗流连续方程和

实际水文地质条件，建立浅层地下水三维非稳定流数学模型 ［17］ ，公式如下：
ì ∂h ∂∂ æ ∂h ö ∂∂ æ ∂h ö ∂∂ æ ∂h ö
ï μ d ∂t = ∂x è K x ∂x ø + ∂y ç K y ∂y ÷ + ∂z è K z ∂z ø + ε (x，y，z )∈ Ω，t ≥ 0
ï
ï è ø
ï
ïh(x，y，z，t | ) = h (x，y，z ) (x，y，z )∈ Ω
ï
í t = 0 0 （1）
ï h(x，y，z，t | ) = h (x，y，z ) (x，y，z )∈ Ω，t > 0
ï S 1
ï ∂h | 1
ï
ï
ï ∂n | | = 0 (x，y，z )∈ Ω，t > 0
î S 2
— 257 —