Page 100 - 水利学报2021年第52卷第4期

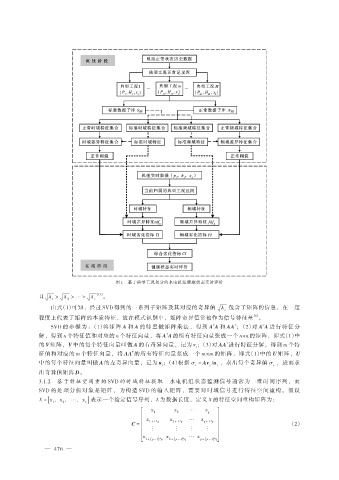
图 1 基于典型工况划分的水电机组健康状态实时评价
且 λ > λ >  > λ ［13］ 。
1 2 r
由式（1）可知，经过 SVD 得到的一系列子矩阵及其对应的奇异值 λ 包含了矩阵的信息，在一定
i
［8］
程度上代表了矩阵的本质特征，故在模式识别中，矩阵奇异值常被作为信号特征量 。
SVD 的步骤为：（1）将矩阵 A 和 A 的转置做矩阵乘法，得到 A A 和 AA ；（2）对 A A 进行特征分
T
T
T
解，得到 n 个特征值和对应的 n 个特征向量，将 A A 的所有特征向量张成一个 n×n 的矩阵，即式（1）中
T
的 V 矩阵，V 中的每个特征向量叫做 A 的右奇异向量，记为 v ；（3）对 AA 进行特征分解，得到 m 个特
T
i
征值和对应的 m 个特征向量，将 AA 的所有特征向量张成一个 m×m 的矩阵，即式（1）中的 U 矩阵，U
T
中的每个特征向量叫做 A 的左奇异向量，记为 u ；（4）根据 σ = Av /u ，求出每个奇异值 σ ，进而求
i
i
i
i
i
出奇异值矩阵 D。
3.1.2 基于特征空间重构 SVD 的时域特征提取 水电机组状态监测信号通常为一维时间序列，而
SVD 的处理分析对象是矩阵，为构造 SVD 的输入矩阵，需要对时域信号进行特征空间重构。假设
X = [x ，x ，，x ] 表示一个给定信号序列，L 为数据长度，定义 X 的特征空间重构矩阵为：
1 2 L
é x x  x q ù
ê ê x 1 x 2  x ú ú
C = ê ê 1 + 1*q 2 + 1*q q + 1*q ú ú （2）
ê ê     ú ú
ê ê x x  x ú ú
ë 1 + ( p - 1 )*q 2 + ( p - 1 )*q q + ( p - 1 )*q û
— 476 —