Page 112 - 2022年第53卷第3期

( )
式中ATE Y k β 为Y k β 的注意熵。

（3）利用式（3）计算所有 k 的 TSMA（k），将这些值的集合作为 TSMATE。
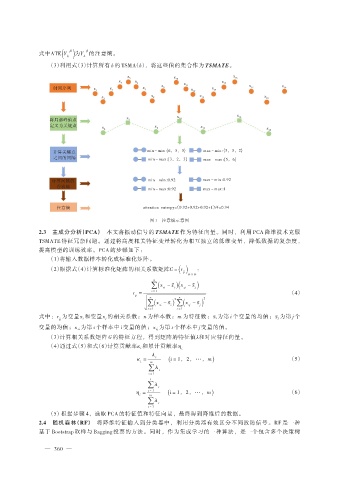
x x x
x 5 x 10 x 16
4 6 x x 15 x x
时间序列 x x x 9 11 x x 17 19
1 3 7 12 14
x x 8 x 13 x
2 18

x x x 16
将局部峰值点 5 10
定义为关键点 x x x
2 8 13 x
18

计算关键点 min - min :{6，5，5 } max - min :{3，3，2 }
之间的间隔 min - max :{3，2，3 } max - max :{5，6 }

计算间隔的 min - min :0.92 max - min :0.92
香农熵
min - max :0.92 max - max :1

注意熵 attention entropy=（0.92+0.92+0.92+1）4=0.94
/
图 1 注意熵示意图
2.3 主成分分析（PCA） 本文将振动信号的 TSMATE 作为特征向量。同时，利用 PCA 降维技术克服
TSMATE 特征冗杂问题。通过将高度相关特征变量转化为相互独立的低维变量，降低数据的复杂度，
提高模型的训练效率。PCA 的步骤如下：
（1）将输入数据样本转化成标准化矩阵。
（2）根据式（4）计算标准化矩阵的相关系数矩阵G = ( ) ：
r
ij
m × m
n
sj
si
å(x - x ˉ i )( x - x ˉ j )
r = s = 1 （4）
ij
n
) 2 n ) 2
si
sj
å(x - x ˉ i å( x - x ˉ j
s = 1 s = 1
式中：r 为变量x i 和变量x j 的相关系数；n 为样本数；m 为特征数；x ˉ i 为第 i 个变量的均值；x ˉ j 为第 j 个
ij
变量的均值；x si 为第 s 个样本中 i 变量的值；x sj 为第 s 个样本中 j 变量的值。
（3）计算相关系数矩阵 G 的特征方程，得到矩阵的特征值λ和对应特征向量。
（4）通过式（5）和式（6）计算贡献率κ i 和累计贡献率η i
λ
κ = m i (i = 1，2，⋯，m ) （5）
i
å λ s
s = 1
i
å λ s
η = s = 1 (i = 1，2，⋯，m ) （6）
i
m
å λ s
s = 1
（5）根据步骤 4，选取 PCA 的特征值和特征向量，最终得到降维后的数据。
2.4 随机森林（RF） 将降维特征输入到分类器中，利用分类器有效区分不同故障信号。RF 是一种
基于 Bootstrap 取样与 Bagging 投票的方法。同时，作为集成学习的一种算法，是一个包含多个决策树

— 360 —