Page 7 - 2023年第54卷第2期

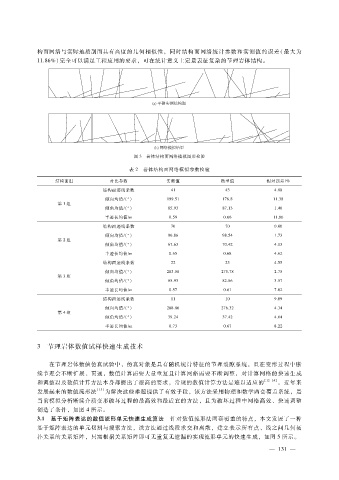
构面网络与实际地质剖面具有高度的几何相似性，同时结构面网络统计参数和实测值的误差（最大为
１１．８６％）完全可以满足工程应用的要求，可在统计意义上定量表征复杂的节理岩体结构。

图 ３ 岩体结构面网络模拟图形检验

表 ２ 岩体结构面网络模拟参数检验
结构面组 对比参数 实测值 模型值 相对误差?％
结构面迹线条数 ４１ ４３ ４．８８
倾向均值?（°） １９９．５１ １７６．８ １１．３８
第 １组
倾角均值?（°） ８５．９３ ８７．１３ １．４０
半迹长均值?ｍ ０．５９ ０．６６ １１．８６
结构面迹线条数 ７０ ７０ ０．００
倾向均值?（°） ９６．８６ ９８．５４ １．７３
第 ２组
倾角均值?（°） ６７．６３ ７０．４２ ４．１３
半迹长均值?ｍ ０．６５ ０．６８ ４．６２
结构面迹线条数 ２２ ２３ ４．５５
倾向均值?（°） ２８３．５８ ２７５．７８ ２．７５
第 ３组
倾角均值?（°） ８５．９３ ８２．８６ ３．５７
半迹长均值?ｍ ０．５７ ０．６１ ７．０２
结构面迹线条数 １１ １０ ９．０９
倾向均值?（°） ２８８．８６ ２７６．３２ ４．３４
第 ４组
倾角均值?（°） ３９．２４ ３７．４２ ４．６４
半迹长均值?ｍ ０．７３ ０．６７ ８．２２

３ 节理岩体数值试样快速生成技术

在节理岩体数值仿真试验中，仿真对象是具有随机统计特征的节理裂隙系统，且在变形过程中断
续节理会不断扩展、贯通，数值计算需要大量重复且计算网格需要不断调整，对计算网格的快速生成
和调整以及数值计算方法本身都提出了很高的要求，常规的数值计算方法是难以适应的 ［１２ － １４］ 。近年来
发展起来的数值流形法 ［１５］ 为解决这些难题提供了有效手段，该方法采用物理和数学两套覆盖系统，是
当前模拟分析断续介质变形破坏过程的最高效和最适宜的方法，且为破坏过程中网格高效、快速调整
创造了条件，如图 ４所示。
３．１ 基于矩阵表达的数值流形单元快速生成算法 针对数值流形法两套覆盖的特点，本文发展了一种
基于矩阵表达的单元切割与搜索方法，该方法通过线段求交和离散，建立表示所有点、线之间几何拓
扑关系的关系矩阵，只需根据关系矩阵即可无重复无遗漏的实现流形单元的快速生成，如图 ５所示。

— １ ３ １ —