Page 9 - 2023年第54卷第2期

周应力来判断裂纹是否启裂以及启裂后的扩展方向，并提出了裂纹扩展与追踪技术，实现了节理岩体
变形破坏全过程模拟。
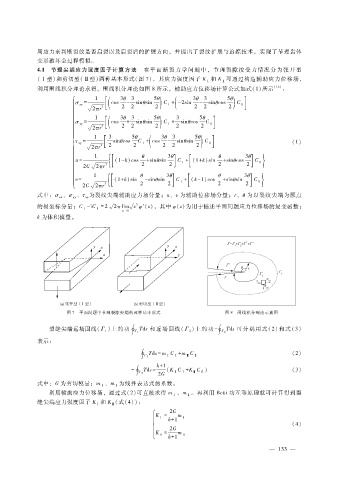
４．１ 节理尖端应力强度因子计算方法 在平面断 裂力学 问 题 中，节 理裂 隙 按 受力 情况 分为 张开型
（ Ⅰ型）和剪切型（ Ⅱ型）两种基本形式（图 ７），其应力强度因子 Ｋ 和 Ｋ 可通过构造辅助应力位移场，
Ⅰ Ⅱ
利用围线积分理论求得。围线积分理论如图 ８所示，辅助应力位移场计算公式如式（１）所示 ［１６］ ：
１ ３ θ ３ ５ θ ３ θ ３ ５ θ
Ｃ
＝ ３ ([ ｃｏｓ － ｓｉｎ θ ｓｉｎ ) ( ) ]
Ｃ ＋ － ２ｓｉｎ － ｓｉｎ θ ｃｏｓ
σ ｘｘ Ⅰ Ⅱ
２ ２ ２ ２ ２ ２
槡 ２ π ｒ
１ ３ θ ３ ５ θ ３ ５ θ
＝ ３ ([ ｃｏｓ ＋ ｓｉｎ θ ｓｉｎ ) Ｃ ＋ ｓｉｎ θ ｃｏｓ Ｃ ]
σ ｙｙ Ⅰ Ⅱ
２ ２ ２ ２ ２
槡 ２ π ｒ
１ ３ ５ θ ３ θ ３ ５ θ
(
＝ [ ｓｉｎ θ ｃｏｓ Ｃ ＋ ｃｏｓ － ｓｉｎ θ ｓｉｎ ) ]
Ｃ
τ ｘｙ （１）
３ ２ ２ Ⅰ ２ ２ ２ Ⅱ
槡 ２ π ｒ
１ θ ３ θ θ ３ θ
ｕ ＝ ３ [{ （１ － ｋ）ｃｏｓ ＋ ｓｉｎ θ ｓｉｎ ] [ ] }
Ｃ ＋ （１ ＋ ｋ）ｓｉｎ ＋ ｓｉｎ θ ｃｏｓ
Ｃ
２ ２ Ⅰ ２ ２ Ⅱ
２Ｇ ２ π ｒ
槡
１ θ ３ θ θ ３ θ
ｖ ＝ ３ [{ （１ ＋ ｋ）ｓｉｎ － ｓｉｎ θ ｓｉｎ ] [ ] }
Ｃ ＋ （ｋ － １ ）ｃｏｓ ＋ ｓｉｎ θ ｓｉｎ
Ｃ
Ⅰ Ⅱ
２ Ｇ ２ π ｒ ２ ２ ２ ２
槡
为裂纹尖端辅助应力场分量；ｕ、ｖ为辅助位移场分量；ｒ、θ 为以裂纹尖端为原点
式中：σ ｘｘ 、σ ｙｙ 、τ ｘｙ
３
的极坐标分量；Ｃ － ｉ Ｃ ＝ ２ ２ πｌｉｍ ｚφ ′（ｚ），其中 φ （ｚ）为用于描述平面问题应力位移场的复变函数；
槡
槡
Ⅰ Ⅱ
ｘ → ０
ｋ为体积模量。

图 ７ 平面问题中节理裂隙尖端的两种基本形式 图 ８ 围线积分理论示意图

）上的功 ∮ ）上的功 － ∮
Ｔｄｓ可分别用式 （２）和式 （３）
裂缝尖端远场围线（ Γ １ Γ １ Ｔｄｓ和近场围线（ Γ ２ Γ ２
表示：
∮ Ⅰ Ⅰ Ⅱ Ⅱ （２）
Ｔｄｓ ＝ ｍ Ｃ ＋ ｍ Ｃ
Γ １
ｋ ＋ １
Ｔｄｓ ＝
－ ∮ （Ｋ Ｃ ＋ Ｋ Ｃ ） （３）
Ⅰ
Ⅰ
Ⅱ
Ⅱ
２ Ｇ
Γ ２
式中：Ｇ为剪切模量；ｍ 、ｍ 为线性表达式的系数。
Ⅰ Ⅱ
利用辅助应力位移场，通过式（２）可直接求得 ｍ 、ｍ 。再利用 Ｂｅｔｔｉ功互等原理就可计算得到裂
Ⅰ Ⅱ
缝尖端应力强度因子 Ｋ 和 Ｋ （式（４））：
Ⅰ Ⅱ
２ Ｇ
Ｋ ＝ ｍ
Ⅰ Ⅰ
ｋ ＋ １
（４）
２ Ｇ
Ｋ ＝ ｍ
Ⅱ Ⅱ
ｋ ＋ １
— １ ３ ３ —