Page 123 - 2023年第54卷第6期

而 ＲＢＦ神经网络会不可避免地出现非最优权 重 等 问 题 ［１４］ 。 本 文 将 三 个 参 数 作 为 粒 子 群 算 法
的优化目标，将三者视为自由运动的粒子，在 Ｎ维 空 间 中 初 始 化 粒 子 的 速 度、 位 置 等 算 法 参 数，
带入适应度函数计算粒子适应度 ｆ，将网络的均方 误 差 式 （６）作 为 适 应 度 函 数 取 最 小 值 为 最 优 适
ｉ
应度
１ １ Ｔ １ Ｚ
２
ｍｉｎＦ（ｘ） ＝ [ ∑ （ｓ－ｙ ） ＋ ∑ （Ｓ －Ｙ） ２ ] （６）
ｉ
ｌ
ｌ
ｉ
２ Ｔ ｉ ＝１ Ｚ ｌ ＝１
式中：Ｔ、Ｚ为训练、测试样本数；ｓ、Ｓ为实际地震动输出；ｙ、Ｙ为预期地震动输出。
ｉ
ｌ
ｉ
ｌ
模型训练过程中通过不断迭代更新粒子及群体的极值 ｐ、ｇ来更新粒子位置 ｘ，迭代公式为
ｉ ｉ ｉ
（ｋ）
（ｋ ＋ １）
ｘ （ｋ ＋ １） ＝ ｘ ＋ ｖ （７）
ｉ
ｉ
ｉ
（ｋ）
（ｋ）
（ｋ）
（ｋ）
（ｋ）
（ｋ ＋ １ ）
ｖ ＝ ω ｖ ＋ ｃｒ（ｐ － ｘ ） ＋ ｃｒ（ｇ － ｘ ） （８）
ｉ
ｉ
２ ２
１ １
ｉ
ｉ
ｉ
ｉ
式中：ｋ为迭代次数；ω为权值；ｃ为加速度常数；ｒ为［０，１］内的随机数。
２．３ 云理论 优 化 （ＣＰＳＯ－ ＲＢＦ） 粒 子 群 算 法 会 陷 入 非 要 求 的 局 部 极 值，且 存 在 收 敛 速 度 慢 等 问
题 ［１５］ 。为此，本文引入云理论（ＣｌｏｕｄＴｈｅｏｒｙ） ［１６ － １７］ ，对陷入局部极值的粒子进行变异操作。首先给定
参数距离 Ｄ和代数 Ｇ，若粒子在 Ｇ代没有位置变化，或变化值小于 Ｄ时，就判定其陷入局部极值；定
义三个云数字特征对粒子进行变异，将全局极值 Ｇ 作为期望 Ｅ；熵 Ｅ为粒子变异的搜索域，将其设
ｂｅｓｔ ｘ ｎ
置为 ３Ｇ ；超熵 Ｈ为云散度，为了保证算法的鲁棒性，不宜过大或过小，令 Ｈ ＝ Ｅ?１０以保证算法的
ｂｅｓｔ
ｎ
ｅ
ｅ
稳定性和准确性；再将变异后的粒子进行范围寻优以得到最优解。其中变异判定由式（９）决定。云粒
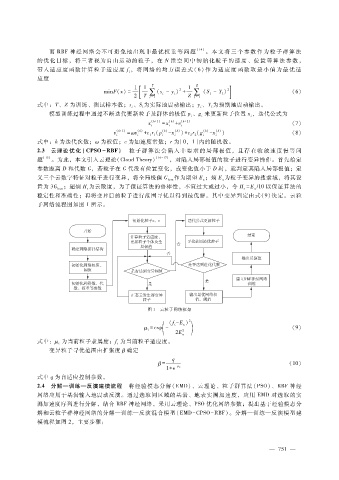
子网络流程图如图 １所示。
图 １ 云粒子网络框架
( （ｆ － Ｅ） ２
２ )
ｉ
ｘ
＝ ｅｘｐ－ （９）
μ ｉ ２Ｅ ｎ
为当前粒子隶属度；ｆ为当前粒子适应度。
式中：μ ｉ
ｉ
变异粒子寻优范围由扩张度 β 确定
ｑ
β ＝ （１０）
１ ＋ ｅ
－ μ ｉ
式中 ｑ为自适应控制参数。
２．４ 分解—训练—反演建模流程 将经验模态分解（ＥＭＤ）、云理论、粒子群算法（ＰＳＯ）、ＲＢＦ神经
网络应用于基岩输入地震动反演。通过选取同区域的基岩、地表实测加速度，应用 ＥＭＤ对选取的实
测加速度序列进行分解，结合 ＲＢＦ神经网络，采用云理论、ＰＳＯ优化网络参数；提出基于经验模态分
解和云粒子群神经网络的分解—训练—反演混合模型（ＥＭＤ － ＣＰＳＯ － ＲＢＦ）。分解—训练—反演模型建
模流程如图 ２，主要步骤：

— ７ ５ １ —