Page 118 - 2023年第54卷第6期

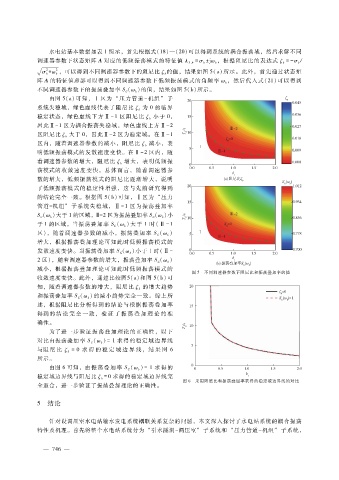
水电站基本数据如表 １所示，首先根据式（１８）—（２０）可以得到系统的耦合振荡域，然后求解不同
?
调速器参数下状态矩阵 Ａ对应的低频振荡模式的特征值 λ ３，４ σ ｂ ω ｂ ＝－ σ ｂ
＝ ±ｊ ，根据阻尼比的表达式 ζ ｂ
２ ２
槡 ＋ ，可以得到不同调速器参数下的阻尼比 ζ ｂ 的值，结果如图 ５（ａ）所示。此外，首先通过状态矩
σ ｂ ω ｂ
，然后代入式（２１）可以得到
阵 Ａ的特征值虚部可以得到不同调速器参数下低频振荡模式的角频率 ω ｂ
）的值，结果如图 ５（ｂ）所示。
不同调速器参数下的振荡叠加率 Ｓ（ ω ｂ
Ｇ
由图 ５（ａ）可知，Ⅰ区为 “压力管道 － 机组” 子
为 ０的临界
系统失稳域，绿色虚线代表了阻尼比 ζ ｂ
小于 ０，
稳定状态，绿色虚线下方Ⅱ － １区阻尼比 ζ ｂ
因此Ⅱ － １区为耦合振荡失稳域，绿色虚线上方Ⅱ － ２
大于 ０，因此Ⅱ － ２ 区为稳定域。在Ⅱ － １
区阻尼比 ζ ｂ
减小，表
区内，随着调速器参数的减小，阻尼比 ζ ｂ
明低频振荡模式的发散速度变快。在Ⅱ － ２区内，随
增大，表明低频振
着调速器参数的增大，阻尼比 ζ ｂ
荡模式的收敛速度变快。总体而言，随着调速器参
数的增大，低频振荡模式的阻尼比逐渐增大，说明
了低频振荡模式的稳定性增强，这与先前研究得到
的结论完全一致。根据图 ５（ｂ）可知，Ⅰ区为 “压力
管道－ 机组” 子系统失稳域，Ⅱ － １区为振荡叠加率
）小
Ｇ
Ｓ（ ω ｂ ）大于 １的区域， Ⅱ － ２ 区为振荡叠加率 Ｓ（ ω ｂ
Ｇ
）大于 １时 （ Ⅱ － １
于 １的区域。当振荡叠加率 Ｓ（ ω ｂ
Ｇ
）
区），随着调速器参数的减小，振荡叠加率 Ｓ（ ω ｂ
Ｇ
增大，根据振荡叠加理论可知此时低频振荡模式的
）小于 １时（ Ⅱ －
Ｇ
发散速度变快。当振荡叠加率 Ｓ（ ω ｂ
）
２区），随着调速器参数的增大，振荡叠加率 Ｓ（ ω ｂ
Ｇ
减小，根据振荡叠加理论可知此时低频振荡模式的
图 ５ 不同调速器参数下阻尼比和振荡叠加率的值
收敛速度变快。此外，通过比较图５（ａ）和图 ５（ｂ）可
的增大趋势
知，随着调速器参数的增大，阻尼比 ζ ｂ
）的减小趋势完全一致。综上所
和振荡叠加率 Ｓ（ ω ｂ
Ｇ
述，根据阻尼比分析得到的结论与根据振荡叠加率
得到 的 结 论 完 全 一 致， 验 证 了 振 荡 叠 加 理 论 的 准
确性。
为了进一步验证振荡叠加理论的正确性，以下
） ＝１求得的稳定域边界线
Ｇ
对比由振荡叠加率 Ｓ（ ω ｂ
＝０求 得 的 稳 定 域 边 界 线， 结 果 图 ６
与阻 尼 比 ζ ｂ
所示。
） ＝１求得的
由图 ６可知，由振荡叠加率 Ｓ（ ω ｂ
Ｇ
＝ ０ 求得的稳定域边界线完
稳定域边界线与阻尼比 ζ ｂ
图 ６ 采用阻尼比和振荡叠加率求得的稳定域边界线的对比
全重合，进一步验证了振荡叠加理论的正确性。
５ 结论

针对设调压室水电站输水发电系统耦联关系复杂的问题，本文深入探讨了水电站系统的耦合振荡
特性及机理。首先将整个水电站系统分为 “引水隧洞－ 调压室” 子系统和 “压力管道 － 机组” 子系统，

— ７ ４ —
６