Page 115 - 2023年第54卷第6期

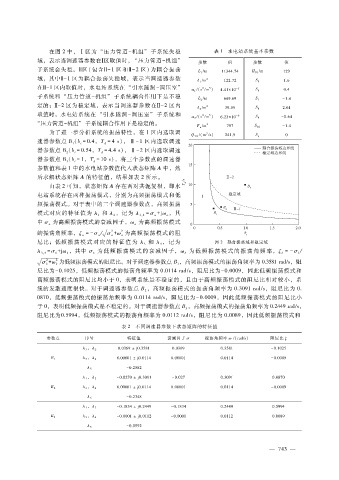
在图 ２中，Ⅰ区为 “压力管道 － 机组” 子系统失稳 表 １ 水电站系统基本参数
域，表示当调速器参数在 Ⅰ 区取值时， “压力管道－ 机组” 参数 值 参数 值
子系统会失稳。 Ⅱ 区（包含Ⅱ － １区和Ⅱ － ２区）为耦合振荡 Ｌ １ ?ｍ １１３４４．７４ Ｈ Ｔ０ ?ｍ １２９
域，其中 Ⅱ － １区为耦合振荡失稳域，表示当调速器参数 Ａ １ ?ｍ ２ １２２．７２ Ｓ ５ １．６
在 Ⅱ － １ 区内取值时，水电站系统在 “引水隧洞－ 调压室” ２ ５
α １ ?（ｓ?ｍ ） ４．４１ × １０ － ５ Ｓ ６ ０．４
子系统和 “压力管道－ 机组” 子系统耦合作用下是不稳 Ｌ ２ ?ｍ ６４９．６９ Ｓ ７ － １．４
定的； Ⅱ － ２ 区为稳定域，表示当调速器参数在Ⅱ － ２区内 ２
Ａ ２ ?ｍ ３９．５９ Ｓ ８ ２．６４
取值时，水电站系统在 “引水隧洞 － 调压室” 子系统和 ２ ５
α ２ ?（ｓ?ｍ ） ６．２３ × １０ － ６ Ｓ ９ － ０．６４
“压力管道－ 机组”子系统耦合作用下是稳定的。
Ｆ ｕ ?ｍ ２ ７８７ Ｓ １０ － １．４
为了进一步分析系统的振荡特性，在Ⅰ区内选取调
３
Ｑ Ｔ０ ?（ｍ ?ｓ） ２４１．９ Ｓ ｐ ０
速器参数点 Ｂ（ｂ＝ ０ ．４，Ｔ ＝ ４ｓ ），Ⅱ － １区内选取调速
１
ｄ
ｔ
器参数点 Ｂ（ｂ＝ ０．５４，Ｔ ＝ ４．４ｓ），Ⅱ － ２区内选取调速
２ ｔ ｄ
器参数点 Ｂ（ｂ＝ １ ，Ｔ ＝ １０ｓ ），将三个参数点的调速器
３ ｔ ｄ
参数值和表 １中的水电站参数值代入状态矩阵 Ａ中，然
后求解状态矩阵 Ａ的特征值，结果如表 ２所示。
由表 ２可知，状态矩阵 Ａ存在两对共轭复根，即水
电站系统存在两种振荡模式，分别为高频振荡模式和低
频振荡模式。对于表中的三个调速器参数点，高频振荡
＝ ＋ ｊ ，其
模式对应的特征值为 λ １ 和 λ ２ ，记为 λ １，２ σ ａ ω ａ
为高频振荡模式
中 σ ａ 为高频振荡模式的衰减因子，ω ａ
２ ２
＋ 为高频振荡模式的阻
槡
的振荡角频率，ζ ａ ＝－ σ ａ ? σ ａ ω ａ
，记 为 图 ２ 耦合振荡域和稳定域
尼比；低频 振 荡 模 式 对 应 的 特 征 值 为 λ ３ 和 λ ４
?
＝ ＋ ｊ ，其中 σ ｂ
λ ３，４ σ ｂ ω ｂ 为 低 频 振 荡 模 式 的 衰 减 因 子，ω ｂ 为 低 频 振 荡 模 式 的 振 荡 角 频 率，ζ ｂ ＝－ σ ｂ
２
２ ＋ 为低频振荡模式的阻尼比。对于调速器参数点 Ｂ，高频振荡模式的振荡角频率为 ０．３５８１ｒａｄ?ｓ，阻
槡 １
σ ｂ ω ｂ
尼比为－ ０．１０２５ ，低频振荡模式的振荡角频率为 ０．０１１４ｒａｄ?ｓ，阻尼比为－ ０．０００９ ，因此低频振荡模式和
高频振荡模式的阻尼比均小于 ０，表明系统是不稳定的，且由于高频振荡模式的阻尼比相对较小，系
统的发散速度很快。对于调速器参数点 Ｂ，高频振荡模式的振荡角频率为 ０．３０９１ｒａｄ?ｓ，阻尼比为 ０．
２
０８７０，低频振荡模式的振荡角频率为 ０．０１１４ｒａｄ?ｓ，阻尼比为 － ０．０００９ ，因此低频振荡模式的阻尼比小
于 ０，表明低频振荡模式是不稳定的。对于调速器参数点 Ｂ，高频振荡模式的振荡角频率为 ０．２４４９ｒａｄ?ｓ，
３
阻尼比为０．５９９４，低频振荡模式的振荡角频率为 ０．０１１２ｒａｄ?ｓ，阻尼比为 ０．００８９，因此低频振荡模式和
表 ２ 不同调速器参数下状态矩阵的特征值

参数点 序号 特征值 衰减因子 σ 振荡角频率 ω?（ｒａｄ?ｓ） 阻尼比 ζ
０．０３６９±ｊ０．３５８１ ０．０３６９ ０．３５８１ － ０．１０２５
λ １ ，λ ２
０．００００１±ｊ０．０１１４ ０．００００１ ０．０１１４ － ０．０００９
Ｂ １ λ ３ ，λ ４
－ ０．２５８２
λ ５
－ ０．０２７０±ｊ０．３０９１ － ０．０２７ ０．３０９１ ０．０８７０
λ １ ，λ ２
０．００００１±ｊ０．０１１４ ０．００００１ ０．０１１４ － ０．０００９
Ｂ ２ λ ３ ，λ ４
－ ０．２３４８
λ ５
－ ０．１８３４±ｊ０．２４４９ － ０．１８３４ ０．２４４９ ０．５９９４
λ １ ，λ ２
－ ０．０００１±ｊ０．０１１２ － ０．０００１ ０．０１１２ ０．００８９
Ｂ ３ λ ３ ，λ ４
－ ０．０５９２
λ ５

— ７ ４ ３ —