Page 67 - 2024年第55卷第6期

图 ７ 轴向渗透条件下体积应变与渗透系数关系曲线

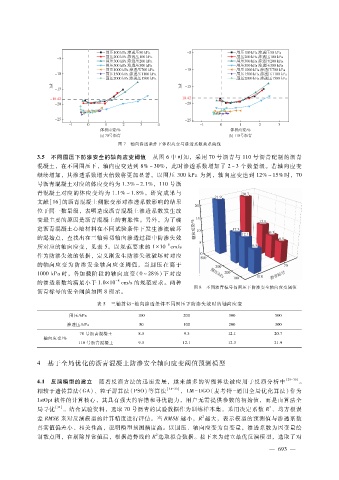
３．５ 不同围压下防渗安全的轴向应变阈值 从图 ６中可知，采用 ７０号沥青与 １１０号沥青配制的沥青
混凝土，在不同围压下，轴向应变达到 ８％～３０％，此时渗透系数增加了 ２～３个数量级。若轴向应变
继续增加，其渗透系数增大倍数将更加显著。以围压 ３００ｋＰａ为例，轴向应变达到 １２％～１５％时，７０
号沥青混凝土对应的体应变约为 １．３％～２．１％，１１０号沥
青混凝土对应的体应变约为 １．１％～１．８％。研究成果与
文献［ １６］的沥青混凝土侧胀变形对渗透系数影响的结果
位于同一数量级，表明造成沥青混凝土渗透系数发生改
变最主要的原因是沥青混凝土的剪胀性。另外，为了确
定沥青混凝土心墙材料在不同试验条件下发生渗流破坏
的起始点，查找出在三轴剪切轴向渗透过程中防渗失效
－ ８
所对应的轴向应变，见表 ５。以规范要求的 １ × １０ ｃｍ?ｓ
作为防渗失效的依据，定义刚发生防渗失效破坏时对应
的轴向应 变 为防 渗安 全轴向 应变 阈值，当 围 压 在 高 于
１０００ｋＰａ时，各加载阶段的轴向应变（０～２８％）下对应
－ ８
的渗透系数均满足小于 １．０ × １０ ｃｍ?ｓ的规范要求。两种
图 ８ 不同沥青标号各围压下防渗安全轴向应变阈值
沥青标号的安全阈值如图 ８所示。
表 ５ 三轴剪切－ 轴向渗透条件不同围压下防渗失效时的轴向应变

围压?ｋＰａ １００ ２００ ３００ ５００
渗透压?ｋＰａ ５０ １００ ２００ ３００
７０号沥青混凝土 ８．５ ９．３ １２．１ ２０．７
轴向应变?％
１１０ 号沥青混凝土 ９．５ １２．１ １２．３ ２１．９

４ 基于全局优化的沥青混凝土防渗安全轴向应变阈值预测模型

４．１ 反演模型的建立 随着反演方法的迅速发展，越来越多的智能算法被应用于反演分析中 ［２９ － ３０］ 。
相较于遗传算法（ＧＡ）、粒子群算法（ＰＳＯ）等算法 ［３１ － ３３］ ，ＬＭ－ ＵＧＯ（麦考特 － 通用全局优化算法）作为
１ｓｔＯｐｔ软件的计算核心，其具有强大的容错和寻优能力，用户无需提供参数的初始值，而是由算法全
２
局寻优 ［３４］ 。结合试验资料，选取 ７０号沥青的试验数据作为训练样本集，采用决定系数 Ｒ、均方根误
２
差 ＲＭＳＥ来对反演模型的计算精度进行评估。当 ＲＭＳＥ越小，Ｒ越大，表示模型的预测值与渗透系数
真实值偏差小、相关性高，说明模型预测精度高。以围压、轴向应变为自变量，渗透系数为因变量绘
２
制散点图，在剔除异常值后，根据趋势线的 Ｒ选取拟合数据。接下来为建立最优反演模型，选取了对
— ６ ９ ３ —