Page 71 - 2024年第55卷第11期

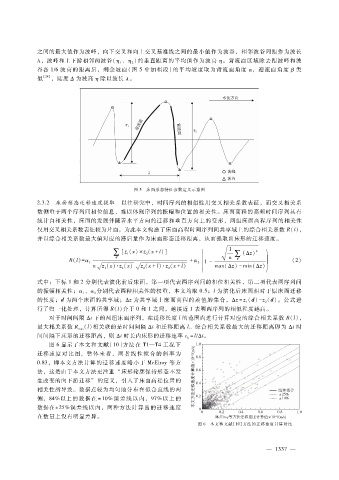
之间的最大值作为波峰，向下交叉和向上交叉基准线之间的最小值作为波谷，相邻波谷间距作为波长
、 ）的垂直距离的平均值作为波高 η 。背流面区域除去距波峰和波
λ ，波峰和上下游相邻两波谷（ η １ η ２
谷各 １?６波高的距离后，剩余坡面（图 ５中加粗段）的平均坡度取为背流面角度 α ，迎流面角度 β类
似 ［２４］ ，陡度 Δ为波高 η除以波长 λ 。

图 ５ 床面形态特征参数定义示意图

２．３．２ 床面形态迁移速度提取 以往研究中，时间序列的相似性用交叉相关系数表征，而交叉相关系
数侧重于两个序列间相位信息，难以体现序列的振幅和位置的相关性。床面高程的高频时间序列具有
统计自相关性，床面的发展伴随着水平方向的迁移和垂直方向上的变形，两组床面高程序列的相关性
仅用交叉相关系数表征较为片面，为此本文构造了床面高程时间序列间共享域上的综合相关系数 Ｒ（ｌ），
并以综合相关系数最大值对应的滞后量作为床面形态迁移距离，从而提取出床形的迁移速度。
１
∑ ［ｚ（ｘ） × ｚ（ｘ ＋ ｌ）］ ∑ （ Δ ｚ） ２
１
２
ｄ 槡
ｎ ｄ
＋ α ２ １－ （２）
Ｒ（ｌ） ＝ α １
ｎ ｚ（ｘ）·ｚ（ｘ） ｚ（ｘ ＋ ｌ）·ｚ（ｘ ＋ ｌ） ｍａｘ（ Δ ｚ） － ｍｉｎ（ Δ ｚ）
槡 １ １ 槡 ２ ２
式中：下标 １和 ２分别代表演化前后床面，第一项代表两序列间的相位相关性，第二项代表两序列间
分别代表两种相关性的权重，本文均取 ０．５；ｌ为演化后床面相对于原床面迁移
的振幅相关性；α １ 、α ２
的长度；ｄ为两个床面的共享域；Δ ｚ为共享域上床面高程的差值的集合，Δ ｚ ＝ ｚ（ｄ） － ｚ（ｄ）。公式进
２
１
行了归一化处理，计算所得 Ｒ（ｌ）介于 ０和 １之间，越接近 １表明两序列的相似程度越高。
对于时间间隔 Δ ｔ下的两组床面序列，在迁移长度 ｌ的范围内进行计算对应的综合相关系数 Ｒ（ｌ），
最大相关系数 Ｒ （ｌ）相关联的是时间间隔 Δ ｔ和迁移距离 ｌ。综合相关系数最大的迁移距离即为 Δ ｔ时
ｍａｘ
间间隔下床形的迁移距离，则 Δ ｔ时长内床形的迁移速率 ｃ＝ ｌ? Δ ｔ。
ｂ
图 ６显示了本文和文献［１０］方法在 Ｔ１—Ｔ４工况下
迁移速 度 对 比 图，整体 来看，两者 线性拟 合 的 斜 率 为
０．８３，即本文方法计算的迁移速度略小于 ＭｃＥｌｒｏｙ等方
法，这是由于本文方法更注重 “床形轮廓保持形态不发
生改变的向下游迁移” 的定义，引入了床面高程位置的
相关性所导致。数据点较为均匀地分布在拟合直线的两
侧，８４％以上的数据在 ±１０％误 差线 以内，９７％以上 的
数据在±２５％误差线以内，两种方法计算出的迁移速度
在数量上没有明显差异。
图 ６ 本文和文献［１０］方法的迁移速度计算对比

３
— １ ３ ７ —