Page 76 - 2024年第55卷第11期

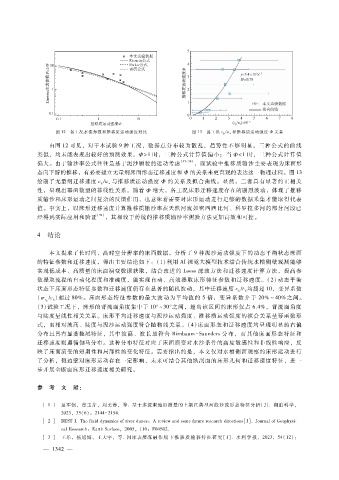
图 １２ 各工况水流参数和推移质运动强度对比 图 １３ 各工况 ｃ ｂ ?ｕ 和推移质运动强度 Φ 关系

由图 １２可见，对于本试验 ９种工况，数据点分布较为散乱，趋势性不够明显。三种公式的曲线
类似，均未能表现出较好的预测效果。Φ＞１时，三种公式计算值偏小；当 Φ＜１时，三种公式计算值
偏大。由于输沙率公式往往是基于泥沙颗粒的运动考虑 ［３７ － ３８］ ，而试验中推移质输沙主要表现为床面形
态向下游的推移，有必要建立无量纲床面形态迁移速度和 Φ的关系来更直观的表达这一物理过程。图 １３
绘制了无量纲迁移速度 ｃ?ｕ 与推移质运动强度 Φ 的关系及拟合曲线。显然，二者具有显著的正相关
ｂ

性，呈现出幂函数型的非线性关系。随着 Φ 增大，各工况床形迁移速度存在的剧烈波动，体现了推移
质输沙和床形运动之间复杂的反馈作用，也意味着需要对床形运动进行足够的数据采集才能取得代表
值。事实上，以床形迁移速度计算推移质输沙率在天然河流如密西西比河、科罗拉多河的部分河段已
经得到实际应用和验证 ［３９］ ，其相较于传统的推移质输沙率测验方法更加高效和可控。

４ 结论

本文提取了长时间、高时空分辨率的床面数据，分析了 ９种泥沙运动强度下的动态平衡状态床面
的特征参数和迁移速度，得出主要结论如下：（ １）利用 ＡＩ视觉大模型技术结合传统水槽侧壁观测能够
实现低成本、高质量的床面演变数据获取，结合改进的 Ｌｏｅｓｓ滤波方法和迁移速度计算方法，提高参
数提取流程的自动化程度和准确度，能实现自动、高效提取床形特征参数和迁移速度。（ ２）动态平衡
ｃ均超过 １０，变异系数
状态下床面形态特征参数和迁移速度仍存在显著的随机波动，其中迁移速度 ｃ? 珋
ｂ ｂ
ｃ）超过 ８０％。床面形态特征参数的最大波动为平均值的 ５倍，变异系数介于 ２０％～４０％之间。
? 珋
（ σ ｃ ｂ ｂ
（ ３）试验工况下，床形的背流面角度集中于 １０°～３０°之间，超出该区间的床形仅占 ６．４％，背流面角度
与陡度呈线性相关关系。床形平均迁移速度与泥沙运动强度、推移质运动强度的拟合关系呈幂函数形
式，而相对波高、陡度与泥沙运动强度符合抛物线关系。（ ４）床面形态和迁移速度均呈现明显的右偏
分布且具有显著拖尾特征，其中波高、波长最符合 Ｂｉｒｎｂａｕｍ－ Ｓａｕｎｄｅｒｓ分布，而其他床面形态特征和
迁移速度则遵循伽马分布。这种分布特征对应了床面演变对水沙条件的高度敏感性和非线性响应，反
映了床面演变的短期性和局部性的变化特征。需要指出的是，本文仅对水槽侧面观察的床形运动进行
了分析，侧边壁对床形运动存在一定影响，未来可结合其他纵剖面的床形几何和迁移速度特征，进一
步开展全断面床形迁移速度相关研究。

参 考 文 献：

［ １］ 夏军强，曹玉芹，周美蓉，等．基于多波束地形测量的上荆江典型河段沙波形态特征分析［Ｊ］．湖泊科学，
２０２３，３５（６）：２１４４ － ２１５４．
［ ２］ ＢＥＳＴＪ．Ｔｈｅｆｌｕｉｄｄｙｎａｍｉｃｓｏｆｒｉｖｅｒｄｕｎｅｓ：Ａｒｅｖｉｅｗａｎｄｓｏｍｅｆｕｔｕｒｅｒｅｓｅａｒｃｈｄｉｒｅｃｔｉｏｎｓ［Ｊ］．ＪｏｕｒｎａｌｏｆＧｅｏｐｈｙｓｉ
ｃａｌＲｅｓｅａｒｃｈ：ＥａｒｔｈＳｕｒｆａｃｅ，２００５，１１０：Ｆ０４Ｓ０２．
［ ３］ 王乐，杨旭博，王大宇，等．河床表层冻 融 作 用 下 推 移 质 输 移 特 征 研 究 ［Ｊ］．水 利 学 报，２０２３，５４（１２）：

— １ ３ ２ —
４