Page 75 - 2024年第55卷第11期
P. 75
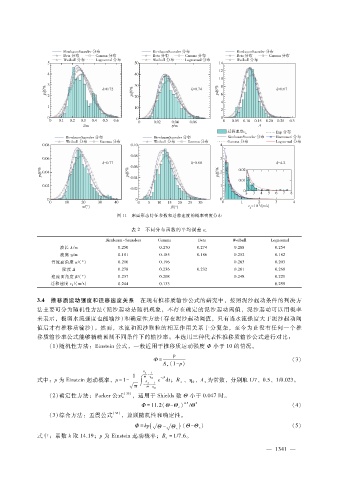
图 11 床面形态特征参数和迁移速度的概率密度分布
表 2 不同分布函数的平均误差 ε
Birnbaum - Saunders Gamma Beta Weibull Lognormal
波长 λ ?m 0.250 0.270 0.274 0.288 0.254
波高 η ?m 0.181 0.185 0.186 0.252 0.182
背流面角度 α ?(°) 0.210 0.196 0.263 0.203
陡度 Δ 0.278 0.236 0.232 0.261 0.268
迎流面角度 β ?(°) 0.237 0.208 0.248 0.221
迁移速度 c b ?(m?s) 0.244 0.133 0.255
3.4 推移质运动强度和迁移速度关系 在现有推移质输沙公式的研究中,按照泥沙起动条件的判决方
法主要可分为随机性方法(泥沙起动是随机现象,不存在确定的泥沙起动阈值,泥沙起动可以用概率
来表示,极弱水流强度也能输沙)和确定性方法(存在泥沙起动阈值,只有当水流强度大于泥沙起动阈
值后才有推移质输沙)。然而,水流和泥沙颗粒的相互作用关系十分复杂,至今为止没有任何一个推
移质输沙率公式能够精确预测不同条件下的输沙率。本选用三种代表性推移质输沙公式进行对比:
( 1)随机性方法:Einstein公式,一般适用于推移质运动强度 Φ 小于 10的情况。
p
Φ= (3)
A (1 - p)
B 1
1 Θ - η - t 2
式中:p为 Einstein起动概率,p = 1 - 0 e dt;B 、η 0 、A 为常数,分别取 1?7、0.5、1?0.023。
B
∫ 1
槡 π - Θ - η 0
( 2)确定性方法:Parker公式 [35] ,适用于 Shields数 Θ小于 0.047时。
4.5 3
) ? Θ (4)
Φ= 11.2( Θ - Θ c
( 3)综合方法:孟震公式 [36] ,兼顾随机性和确定性。
( ) (5)
槡 槡
Φ= kp Θ- Θ c ) ( Θ - Θ c
式中:系数 k取 14.19;p为 Einstein起动概率;B = 1?7.6 。
3
— 1 4 1 —