Page 87 - 2024年第55卷第11期

通过电站历史数据训练，ＤＱＮ算法已学习得到较稳定的分配策略，因此其可利用神经网络快速决策，
枯水期用时约 ０．９８ｈ、汛期 用时 约 １．０２ｈ，分 别为方案 １的 ０．９１％与 １．０７％；方案 ３将精度提升至
１ＭＷ 后，枯水期、汛期代表月份耗时分别为 １．０１ｈ与 １．０８ｈ，分别为方案 １的 ０．９４％与 １．１３％，计算效
率分别提高约 １０６．４倍和 ８８．２倍。因此，ＤＱＮ算法可显著缩短计算时间，保证电站决策满足时效性要求。

表 ４ 枯水期 ２０２０年 １月节水增发效果表 表 ５ 汛期 ２０２０年 ７月水位控制效果表
方案 末水位?ｍ 总耗水量× １０?ｍ ３ 计算时间?ｓ 方案 最大正偏差?ｍ 最小负偏差?ｍ 方差?ｍ ２ 计算时间?ｓ
６
方案 １ ６２２．０６ １９１６．３６４ ３８７５９１．４９ 方案 １ １．９１ － ３．５４ ０．９１３ ３４１７９９．４４
方案 ２ ６２２．９０ １９１５．２４７ ３５２４．９１ 方案 ２ １．８７ － ３．５２ ０．９１５ ３６５７．２８
方案 ３ ６２３．０９ １９１３．７０４ ３６４３．１２ 方案 ３ １．９０ － ３．５１ ０．８８７ ３８７６．５７
方案 ４ ６１９．８０ １９２１．２１５ ２１８３３．６８ 方案 ４ １．９４ － ３．４６ １．０５６ ２３１６０．２１

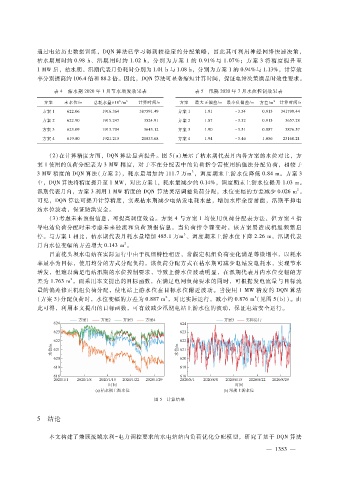
（２）在计算精度方面，ＤＱＮ算法显著提升。图 ５（ａ）展示了枯水期代表月内各方案的水位对比，方
案 １使用的负荷分配表为 ３ＭＷ 精度，对于不在分配表中的负荷指令需使用插值法分配负荷，相较于
３
３ＭＷ 精度的 ＤＱＮ算法（方案 ２），耗水量增加约 １１１．７万ｍ ，调度期末上游水位降低 ０．８４ｍ。方案 ３
中，ＤＱＮ算法将精度提升至 １ＭＷ，对比方案 １，耗水量减少约 ０．１４％，调度期末上游水位提升 １．０３ｍ。
２
汛期代表月内，方案 ３利用 １ＭＷ 精度的 ＤＱＮ算法灵活调整负荷分配，水位变幅的方差减少 ０．０２６ｍ 。
可见，ＤＱＮ算法可提升计算精度，实现枯水期减少电站发电耗水量，增加水库余留蓄能，汛期平抑电
站水位波动，保证防洪安全。
（ ３）考虑未来预报信息，可提高调度效益。方案 ４与方案 １均使用负荷分配表方法，但方案 ４指
导电站负荷分配时未考虑未来径流和负荷预报信息，当负荷指令骤变时，该方案易造成机组频繁启
３
停。与方案 １相比，枯水期代表月耗水量增加 ４８５．１万ｍ 、调度期末上游水位下降 ２．２６ｍ，汛期代表
２
月内水位变幅的方差增大 ０．１４３ｍ 。
目前枕头坝水电站在实际运行中由于机组特性相近，常假定机组负荷变化满足等微增率，以耗水
率最小为目标，使用均分的方式分配负荷。该负荷分配方式在枯水期可减少电站发电耗水，实现节水
增发，但难以满足电站汛期的水位控制要求，导致上游水位波动明显，在汛期代表月内水位变幅的方
２
差为 １．７６３ｍ 。而采用本文提出的目标函数，在满足电网负荷要求的同时，可根据发电流量与目标流
量的偏差修正机组负荷分配，使电站上游水位在目标水位附近波动。当使用 １ＭＷ 精度的 ＤＱＮ算法
２
２
（方案 ３）分配负荷时，水位变幅的方差为 ０．８８７ｍ ，对比实际运行，减小约 ０．８７６ｍ（见图 ５（ｂ））。由
此可得，利用本文提出的目标函数，可有效减少汛期电站上游水位的波动，保证电站安全运行。

图 ５ 计算结果

５ 结论

本文构建了兼顾流域水利－ 电力调控要求的水电站站内负荷优化分配模型，研究了基于 ＤＱＮ算法

３
— １ ５ ３ —