Page 44 - 2025年第56卷第7期

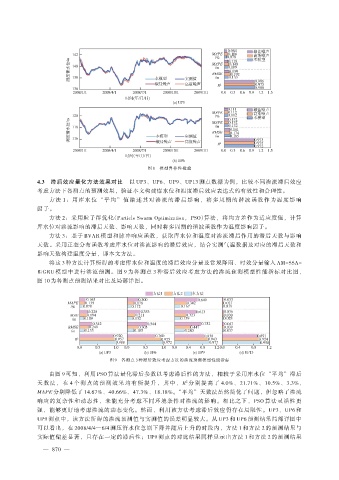
图 8 模型鲁棒性检验

4.3 滞后效应量化方法效果对比 以 UP3、UP6、UP9、UP13 测点数据为例，比较不同渗流滞后效应
考虑方法下各测点的预测效果，验证本文构建库水位和温度滞后效应表达式的有效性和合理性。
方 法 1： 用 库 水 位 “ 平 均 ” 值 描 述 其 对 渗 流 的 滞 后 影 响 ， 将 多 周 期 的 谐 波 函 数 作 为 温 度 影 响
因子。
方法 2：采用粒子群优化（Particle Swarm Optimization，PSO）算法，将均方差作为适应度值，计算
库水位对渗流影响的滞后天数、影响天数，同时将多周期的谐波函数作为温度影响因子。
方法 3：基于 BVAR 模型和脉冲响应函数，获取库水位和温度对渗流滞后作用的滞后天数与影响
天数。采用正态分布函数考虑库水位对渗流影响的滞后效应，结合实测气温数据及对应的滞后天数和
影响天数构建温度分量，即本文方法。
将这 3 种方法计算所得的考虑库水位和温度的滞后效应分量及常规降雨、时效分量输入 AM-SSA-
BiGRU 模型中进行渗流预测。图 9 为各测点 3 种滞后效应考虑方法的渗流预测模型性能指标对比图，
图 10 为各测点预测结果对比及局部详图。

图 9 各测点 3 种滞后效应考虑方法的渗流预测模型性能指标

由图 9 可知，利用 PSO 算法量化滞后参数以考虑滞后性的方法，相较于采用库水位“平均”滞后
天 数 法 ， 在 4 个 测 点 的 预 测 效 果 均 有 所 提 升 ， 其 中 ， R 分 别 提 高 了 4.0%、 21.71%、 10.5%、 3.3%，
2
MAPE 分别降低了 14.67%、40.66%、47.3%、18.18%。“平均”天数法虽然简化了问题，但忽略了渗流
响应的复杂性和动态性，未能充分考虑不同环境条件对渗流的影响。相比之下，PSO 算法灵活性更
强，能够更好地考虑渗流的动态变化。然而，利用该方法考虑滞后效应仍存在局限性。UP3、UP6 和
UP9 测点中，该方法所得的渗流预测值与实测值的误差明显较大。从 UP3 和 UP6 预测结果局部详图中
可以看出，在 2008/4/4—6/4 测压管水位急剧下降并随后上升的时段内，方法 1 和方法 2 的预测结果与
实际值偏差显著，且存在一定的滞后性；UP9 测点的对比结果同样显示出方法 1 和方法 2 的预测结果

— 870 —