Page 139 - 2025年第56卷第8期

种变化需要即时反映在调度计划中。此时，设有 9 辆运输车分别位于“1、2、3、4、5、6、7、8、9”
这些次要节点。根据新的任务需求，后续任务的具体分配为：混凝土施工［'g'］：7，［'m'］：13，渣料
运输［'q'］：11，［'h'］：8，以及其他节点的任务［'a'］：10，［'b'］：9，［'c'］：20，［'d'］：20，［'e'］：
20，［'f'］：10。动态仿真收敛图像如图 8 所示。

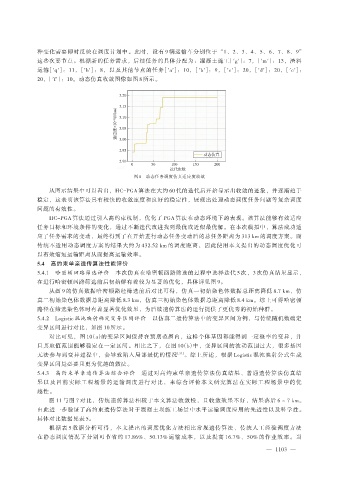
图 8 动态任务调度仿真适应度收敛

从图示结果中可以看出，HC-PGA 算法在大约 60 代的迭代后开始显示出收敛的迹象，并逐渐趋于
稳定，这表明该算法具有较快的收敛速度和良好的稳定性，展现出处理动态调度任务问题等复杂调度
问题的有效性。
HC-PGA 算法通过引入高约束机制，优化了 PGA 算法在动态环境下的表现。该算法能够有效适应
任务目标和环境条件的变化，通过不断迭代改进找到最优或近似最优解。在本次模拟中，算法成功适
应了任务需求的变动，最终得到了在开始进行动态任务变动后的总任务距离为 313 km 的调度方案。而
传统不适用动态调度方案的结果大约为 432.52 km 的调度距离，因此使用本文提出的动态调度优化可
以有效缩短运输距离从而提高运输效率。
5.4 高约束单亲遗传算法性能评价
5.4.1 哈密顿回路筛选评价 本次仿真在哈密顿回路筛选的过程中选择迭代 5 次，3 次仿真结果显示，
在进行哈密顿回路筛选前后初始解有着较为显著的优化，具体详见图 9。
从图 9 的仿真数据哈密顿路经筛选前后对比可得，仿真一初始染色体数据总距离降低 8.7 km，仿
真二初始染色体数据总距离降低 8.3 km，仿真三初始染色体数据总距离降低 8.4 km。综上可得哈密顿
路径在筛选染色体时有着显著优化效果，为后续遗传算法的运行提供了更优秀的初始种群。
5.4.2 Logistic 混沌映射确定变异区间评价 以仿真二遗传算法中的变异区间为例，与传统随机数确定
变异区间进行对比，如图 10 所示。
对比可见，图 10（a）的变异区间保持在预期范围内，这样个体基因都能得到一定概率的变异，并
且其取值范围能够稳定在一定区间。相比之下，在图 10（b）中，变异区间的波动范围过大，很多基因
无法参与到变异过程中，会导致陷入局部最优的情况 ［31］ 。综上所述，根据 Logistic 混沌映射公式生成
变异区间是必要且更为优越的做法。
5.4.3 高约束单亲遗传算法综合评价 通过对高约束单亲遗传算法仿真结果、普通遗传算法仿真结
果以及目前实际工程场景的运输调度进行对比，来综合评价本文研究算法在实际工程场景中的优
越性。
图 11 与图 7 对比，传统遗传算法相较于本文算法收敛慢，且收敛效果不好，结果落后 6 ~ 7 km。
由此进一步验证了高约束遗传算法对于混凝土坝施工场景中水平运输调度应用的先进性以及科学性。
具体对比数据见表 5。
根据表 5 数据分析可得，本文提出的调度优化方法相比常规遗传算法、传统人工经验调度方法
在静态调度情况下分别可节省约 17.86%、50.13% 运输成本，以及提高 16.7%、50% 的作业效率。当

— 1103 —