Page 135 - 2025年第56卷第8期
P. 135
过增加迭代次数来提升哈密顿回路筛选的先进度 [26] 。为了更加直观的表示哈密顿回路筛选初始染色体
组的策略,现将改良圈的图解以原点(即首尾停车点)展开为一条直线,以突出筛选策略的原理。具体
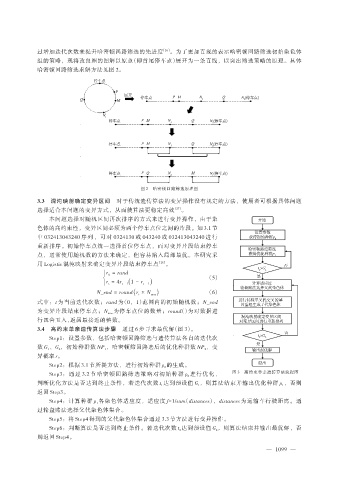
哈密顿回路筛选求解方法见图 2。
图 2 哈密顿回路筛选原理图
3.3 混沌映射确定变异区间 对于传统遗传算法的变异操作没有规定的方法,使用者可根据具体问题
选择适合本问题的变异方式,从而使算法更稳定高效 [27] 。
本问题选择对随机区间再次排序的方式来进行变异操作,由于染
色体的高约束性,变异区间必须为两个停车点位之间的片段。如 3.1 节
中 032413043240 序列,可对 0324130 或 043240 或 032413043240 进 行
重新排序。初始停车点统一选择首位停车点,而对变异片段结束停车
点,通常使用随机数的方法来确定,但容易陷入局部最优。本研究采
用 Logistic 混沌映射来确定变异片段结束停车点 [28] 。
ì r 0 = rand
í ) (5)
î r t = 4r t - 1( 1 - r t - 1
N_end = round( r t × N max) (6)
式中:t 为当前迭代次数;rand 为(0,1)范围内的初始随机数;N_end
为变异片段结束停车点;N 为停车点位的数量;round()为对数据进
max
行四舍五入,返回最接近的整数。
3.4 高约束单亲遗传算法步骤 通过 6 步寻求最优解(图 3)。
Step1:设置参数,包括哈密顿回路筛选与遗传算法各自的迭代次
数 G 、G ,初始种群数 NP ,哈密顿筛回路选后的优化种群数 NP ,变
1 2 1 2
异概率 r。
Step2:根据 3.1 节所提方法,进行初始种群 p 的生成。
0
Step3:通过 3.2 节哈密顿回路筛选策略对初始种群 p 进行优化, 图 3 高约束单亲遗传算法流程图
0
判断优化方法是否达到终止条件,若迭代次数 t 达到预设值 G ,则算法结束并输出优化种群 p ,否则
1 1 1
返回 Step3。
Step4:计算种群 p 各染色体适应度,适应度 f=1/sum(distances),distances 为运输车行驶距离。通
1
过轮盘赌法选择父代染色体集合。
Step5:将 Step4 得到的父代染色体集合通过 3.3 节方法进行变异操作。
Step6:判断算法是否达到终止条件。若迭代次数 t 达到预设值 G ,则算法结束并输出最优解,否
2 2
则返回 Step4。
— 1099 —