Page 55 - 水利学报2021年第52卷第2期

站群优化调度计算，结果见图 4。

（a）水位 （b）出力
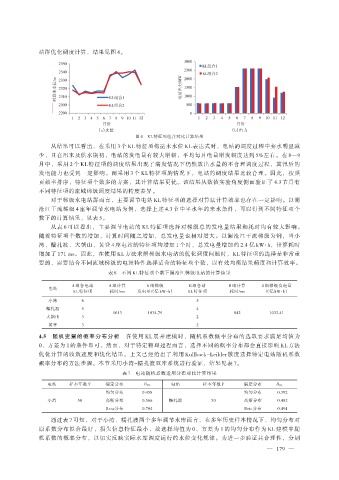
图 4 KL 特征项组合对比计算结果
从结果可以看出，在采用 3 个 KL 特征项构造末水位 KL 表达式时，电站的调度过程中弃水明显减

少，且在汛末及供水期初，电站的发电量有较大增幅，平均每月电量增发幅度达到 5%左右。在 8—9
月中，采用 2 个 KL 特征项的调度结果出现了满发情况下仍然放出水量的不合理调度过程，其汛后的
发电能力也受到一定影响。而采用 3 个 KL 特征项的情况下，电站的调度结果比较合理。因此，按照
贡献率排序，特征项个数多的方案，其计算结果更优。该结果从数值实验角度侧面验证了 4.3 节具有
不同特征项的流域梯级调度结果的精度差异。
对于梯级水电站群而言，主要调节电站 KL 特征项的选择对算法计算效率也存在一定影响。以澜
沧江干流梯级 4 座年调节水电站为例，选择上述 4.3 节中平水年的来水条件，可以得到不同特征项个
数下的计算结果，见表 5。
从表 6 可以看出，主要调节电站的 KL 特征项选择对梯级总的发电量结果和耗时均有较大影响。
随着特征项个数的增加，计算时间随之增加，总发电量也相对增大。以澜沧江干流梯级为例，当小
湾、糯扎渡、大朝山、黄登 4 座电站的特征项均增加 1 个时，总发电量增加约 2.4 亿 kW·h，计算耗时
增加了 171 ms。因此，在使用 KL 方法求解梯级水电站的优化调度问题时，KL 特征项的选择是非常重
要的，需要结合不同流域梯级的电站特性选择适合的特征项个数，以有效均衡结果精度和计算效率。

表 6 不同 KL 特征项个数下澜沧江梯级电站的计算结果
A 组各电站 A 组计算 A 组梯级 B 组各站 B 组计算 B 组梯级发电量
电站
KL 特征项 耗时/ms 发电量/（亿 kW·h） KL 特征项 耗时/ms / （亿 kW·h）
小湾 6 5
糯扎渡 5 4
1013 1034.79 842 1032.41
大朝山 3 2
黄登 3 2
4.5 随机变量的概率分布分析 在使用 KL 展开建模时，随机系数概率分布的选取要求满足均值为
0、方差为 1 的条件即可。然而，对于特定物理过程而言，选择不同的概率分布都会直接影响 KL 方法
优化计算的收敛速度和优化结果。上文已经给出了利用 Kullback-Leibler 散度选择特定电站随机系数
概率分布的方法步骤。本节采用小湾-糯扎渡双库系统进行验证，结果见表 7。

表 7 电站随机系数适用分布对比计算结果
电站 样本年数 Y 假定分布 D KL 电站 样本年数 Y 假定分布 D KL
均匀分布 0.458 均匀分布 0.392
小湾 50 高斯分布 0.566 糯扎渡 50 高斯分布 0.482
Beta 分布 0.704 Beta 分布 0.494
通过表 7 可知，对于小湾、糯扎渡两个多年调节水库而言，在多年历史样本情况下，均匀分布对
原系数分布拟合最好，损失信息特征最小，故选择均值为 0、方差为 1 的均匀分布作为 KL 建模中随
机系数的概率分布，以切实反映实际水库调度运行的水位变化规律。为进一步验证其合理性，分别

— 179 —