Page 68 - 水利学报2021年第52卷第3期

0.60
0.50
0.50
0.40
0.40
残余滑动位移/m 0.30 残余滑动位移/m 0.30

0.20
0.20
0.10 0.10

0.00 0.00
0.0 0.2 0.4 0.6 0.8 1.0 1.2 0.0 0.2 0.4 0.6 0.8 1.0 1.2
加速度×g 加速度×g
（a）不考虑残余凝聚力 （b）考虑残余凝聚力
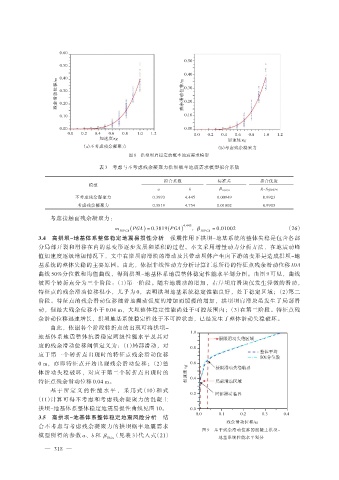
图 8 拱坝坝肩稳定的概率地震需求模型
表 3 考虑与不考虑残余凝聚力拱坝概率地震需求模型拟合系数

拟合系数 标准差 拟合优度
模型
a b β D|PGA R-Square
不考虑残余凝聚力 0.3993 4.445 0.00949 0.9923
考虑残余凝聚力 0.3819 4.754 0.01002 0.9903

考虑接触面残余凝聚力：
)
m D|PGA (PGA = 0.3819(PGA ) 4.445 ，β D|PGA = 0.01002 （26）
3.4 高拱坝-地基体系整体稳定地震易损性分析 强震作用下拱坝-地基系统的整体失稳是包含各部

分局部开裂和滑移在内的总变形逐步发展和累积的过程。本文采用增量动力分析方法，在地震动峰
值加速度逐级增加情况下，文中右岸坝肩滑块的滑动及其带动坝体产生向下游的变形是造成拱坝-地
基系统的整体失稳的主要原因。由此，依据非线性动力分析计算汇总所得的特征点残余滑动位移 IDA
曲线 50%分位数和均值曲线，得到拱坝-地基体系地震整体稳定性能水平划分图。由图 9 可见，曲线
被两个转折点分为三个阶段：（1）第一阶段。随着地震动的增加，右岸坝肩滑块仅发生轻微的滑动，
特征点的残余滑动位移很小，几乎为 0，表明拱坝地基系统稳定性能良好，处于稳定区域；（2）第二
阶段。特征点的残余滑动位移随着地震动强度的增加而缓慢的增加，拱坝坝肩滑块虽发生了局部滑
动，但最大残余位移小于 0.04 m，大坝整体稳定性能尚处于可控范围内；（3）在第三阶段。特征点残
余滑动位移迅速增长，拱坝地基系统稳定性处于不可控状态，已经发生了整体滑动失稳破坏。

由此，依据各个阶段转折点的出现可将拱坝-
1.0
地基体系地震整体抗滑稳定两级性能水平及其对
应的残余滑动位移阈值定义为：（1）局部滑动，对
0.8
应于第一个转折点出现时的特征点残余滑动位移
0 m，亦即特征点开始出现残余滑动位移；（2）整 0.6
体滑动失稳破坏，对应于第二个转折点出现时的 加速度×g
特征点残余滑动位移 0.04 m。 0.4
基 于 所 定 义 的 性 能 水 平 ， 采 用 式（10）和 式
0.2
（11）计算可得不考虑和考虑残余凝聚力的混凝土
拱坝-地基体系整体稳定地震易损性曲线见图 10。 0.0
3.5 高拱坝-地基体系整体稳定地震风险分析 结 0.0 0.1 0.2 0.3 0.4
残余滑动位移/m
合不考虑与考虑残余凝聚力的拱坝概率地震需求
图 9 基于残余滑动位移的混凝土拱坝-
模型所得的参数 a、b 和 β D|im （见表 3）代入式（21） 地基系统性能水平划分

— 318 —