Page 67 - 水利学报2021年第52卷第3期

1.0 1.0
0.8 0.8
0.6 0.6
0.4 0.4
加速度×g 0.2 加速度×g 0.2
0.0
0.0
-0.2
-0.4 -0.2
-0.4
-0.6 -0.6
-0.8 -0.8
-1.0 -1.0
0 4 8 12 16 20 24 28 0 4 8 12 16 20 24 28
时间/s 时间/s
（a） 顺河向加速度时程 （b） 横河向加速度时程
1.0
0.8
0.6
0.4
加速度×g 0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
0 4 8 12 16 20 24 28
时间/s
（c） 竖向加速度时程
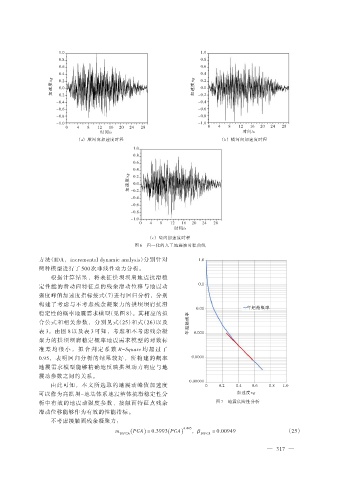
图 6 归一化的人工地震波时程曲线
方法（IDA，incremental dynamic analysis）分别针对 1.0
两种模型进行了 500 次非线性动力分析。
根据计算结果，将表征拱坝坝肩地震抗滑稳
定性能的滑动面特征点的残余滑动位移与地震动 0.1
强度峰值加速度指标按式（7）进行回归分析，分别
构建了考虑与不考虑残余凝聚力的拱坝坝肩抗滑
0.01 年超越概率
稳定性的概率地震需求模型（见图 8）。其相应的拟
合公式和相关参数，分别见式（25）和式（26）以及 年超越概率
表 3。由图 8 以及表 3 可知，考虑和不考虑残余凝 0.001
聚力的拱坝坝肩稳定概率地震需求模型的对数标
准 差 均 很 小 ， 拟 合 判 定 系 数 R-Square 均 超 过 了
0.95，表明回归分析的结果较好，所构建的概率 0.0001
地震需求模型能够精确地反映拱坝动力响应与地
震动参数之间的关系。
0.00001
由此可知，本文所选取的地震动峰值加速度 0 0.2 0.4 0.6 0.8 1.0
可以作为高拱坝-地基体系地震整体抗滑稳定性分 加速度×g
析中有效的地震动强度参数，接触面特征点残余 图 7 地震危险性分析
滑动位移能够作为有效的性能指标。
不考虑接触面残余凝聚力：
)
m D|PGA (PGA = 0.3993(PGA ) 4.445 ，β D|PGA = 0.00949 （25）

— 317 —