Page 50 - 水利学报2021年第52卷第4期
P. 50
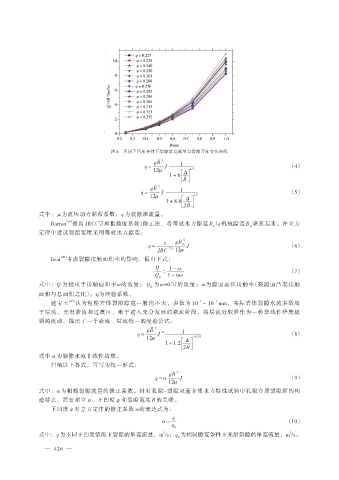
图 8 不同下凹度条件下裂隙单宽流量与裂隙开度变化曲线
gB ˉ 3
q = J 1 (4)
12μ é ù 1.5
Δ
1 + 6 ê ú
ë û ˉ
B
gB ˉ 3
q = J 1 (5)
12μ é Δ ù 1.5
1 + 8.8 ê ú
ë2B ˉ û
式中: μ为流体动力黏滞系数;q 为裂隙渗流量。
[24]
Barton 提出 JRC(节理粗糙度系数)修正法,将等效水力隙宽 B 与机械隙宽 B 联系起来。在立方
h
m
定律中建议裂隙宽度采用等效水力隙宽:
gB 6
q = 1 m J (6)
JRC 7.5 12μ
[46]
Iwai 考虑裂隙接触面积率的影响,提出下式:
Q = 1 - ω
Q 0 1 + ηω (7)
式中:Q 为相应于接触面积率ω的流量; Q 为ω=0 时的流量;ω为隙面面积接触率(裂隙面凸起接触
0
面积与总面积之比);η为经验系数。
速宝玉 [25] 认为粗糙岩体裂隙隙宽一般均不大,多数为 10 ~ 10 mm,实际岩体裂隙水流多数处
-1
-3
于层流、光滑紊流和过渡区,难于进入充分发展的紊流阶段。将层流近似看作为一种非线性程度极
弱的流动,提出了一个紊流、层流统一的经验公式:
gB ˉ 3
q = J m 1 (8)
12μ é Δ ù -0.75
1 + 1.2 ê ú
ë2B ˉ û
式中 m 为裂隙水流非线性指数。
归纳以上各式,可写为统一形式:
gB 3
q = α J (9)
12μ
式中:α 为粗糙裂隙流量的修正系数。针对孔隙-裂隙双重介质水力特性试验中孔隙介质裂隙面的构
造特点,需要建立 α、下凹度 φ 和裂隙宽度 B 的关联。
下凹度 φ 对立方定律的修正系数 α的表达式为:
q
α = (10)
q
0
2
2
式中:q 为不同下凹度情况下裂隙的单宽流量,m /s;q 为相同隙宽条件下光滑裂隙的单宽流量,m /s。
0
— 426 —