Page 52 - 水利学报2021年第52卷第4期

基于立方定律修正系数计算式（14），选取裂隙宽度 B 在 0.02 mm ~ 0.30 mm 间的几组数据进行分
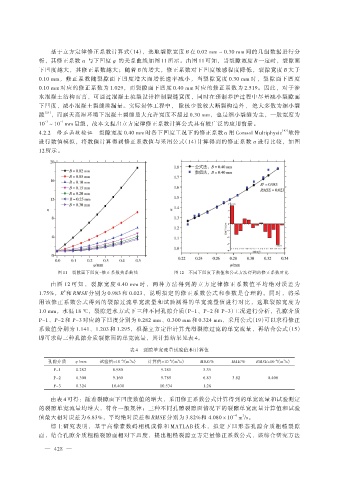
析，其修正系数 α 与下凹度 φ 的关系曲线如图 11 所示。由图 11 可知，当裂隙宽度 B 一定时，裂隙面
下凹度越大，其修正系数越大；随着 B 的增大，修正系数对下凹度敏感程度降低，裂隙宽度 B 大于
0.10 mm，修正系数随裂隙面下凹度增大而增长速率减小，当裂隙宽度 0.30 mm 时，裂隙面下凹度
0.10 mm 对应的修正系数为 1.029，而裂隙面下凹度 0.40 mm 对应的修正系数为 2.519。因此，对于涉
水混凝土结构而言，可通过混凝土抗裂设计控制裂缝宽度，同时在预制养护过程中尽量减小裂隙面
下凹度，减小混凝土裂缝渗漏量。实际岩体工程中， 除极少数较大断裂构造外， 绝大多数为细小裂
隙 ［25］ ，而露天高湿环境下混凝土裂缝最大允许宽度不超过 0.30 mm，也是细小裂缝为主，一般宽度为
-3
-1
10 ~ 10 mm 量级，故本文提出立方定律修正系数计算公式具有较广泛的应用前景。
4.2.2 修正函数验证 裂隙宽度 0.40 mm 时各下凹度工况下的修正系数 α 用 Comsol Multiphysic ［47］ 软件
进行数值模拟，将数值计算得到修正系数值与采用公式（14）计算得到的修正系数 α 进行比较，如图
12 所示。

图 11 裂隙面下凹度-修正系数关系曲线 图 12 不同下凹度下数值和公式方法得到的修正系数对比
由 图 12 可 知 ， 裂 隙 宽 度 0.40 mm 时 ， 两 种 方 法 得 到 的 立 方 定 律 修 正 系 数 值 平 均 绝 对 误 差 为
2
1.75%，R 和 RMSE 分别为 0.983 和 0.023，说明拟定的修正系数公式和参数是合理的。同时，将采
用该修正系数公式得到的裂隙过流单宽流量和试验测得的单宽流量值进行对比，选取裂隙宽度为
1.0 mm，水温 18 ℃，裂隙进水方式下三种不同孔隙介质（P-1、P-2 和 P-3）工况进行分析，孔隙介质
P-1、P-2 和 P-3 对应的下凹度分别为 0.282 mm、0.300 mm 和 0.324 mm，采用公式（19）可以求得修正
系数值分别为 1.141、1.203 和 1.295，根据立方定律计算光滑裂隙过流的单宽流量，再结合公式（15）
即可求得三种孔隙介质裂隙面的单宽流量，其计算结果见表 4。
表 4 裂隙单宽流量试验值和计算值

孔隙介质 φ /mm 试验值×10 /（m /s） 计算值×10 /（m /s） MRE/% MAE/% RMSE×10 /（m /s）
-4
-4
2
-4
2
2
P-1 0.282 8.980 9.281 3.35
P-2 0.300 9.160 9.785 6.83 3.82 0.408
P-3 0.324 10.400 10.534 1.28
由表 4 可得：随着裂隙面下凹度数值的增大，采用修正系数公式计算得到的单宽流量和试验测定
的裂隙单宽流量均增大，符合一般规律；三种不同孔隙裂隙面情况下的裂隙单宽流量计算值和试验
-4 2
值最大相对误差为 6.83%，平均绝对误差和 RMSE 分别为 3.82%和 4.080 × 10 m /s。
综上研究表明，基于高像素数码相机成像和 MATLAB 技术，拟定下凹形态孔隙介质粗糙裂隙
面，结合孔隙介质粗糙裂隙面相对下凹度，提出粗糙裂隙立方定量修正系数公式，该综合研究方法

— 428 —