Page 71 - 2021年第52卷第9期

量 的 相 关 系 数 超 过 0.95， AquaCrop 模 型 效 果 最
2
2
2
差。因此，在动态地下水埋深条件下，采用 BMA 8500 R =0.894 R =0.927 R =0.959
y=0.948x+713.88 y=0.921x+753.74 y=0.996x+62.45
方法 ［29］ 融合 AquaCrop、Jensen 模型的模拟产量能够
提高和平灌区产量模拟精度。 （kg/hm 2 ） 8000
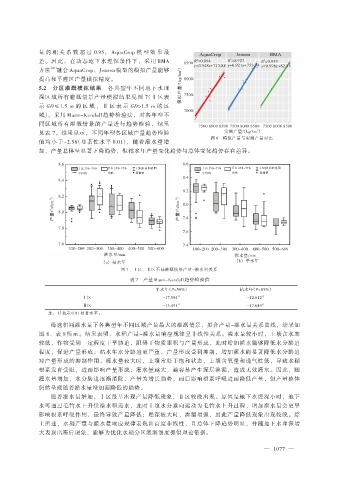
5.2 分区灌溉模拟结果 各典型年不同地下水埋
深区域所有灌溉情景产量模拟结果见图 7（Ⅰ区表 模拟产量/ 7500
示 GD≤1.5 m 的 区 域 ， Ⅱ 区 表 示 GD>1.5 m 的 区
7000
域）。采用 Mann-Kendall 趋势检验法，对各年型不
同区域所有灌溉情景的产量进行趋势检验，结果
7500 8000 8500 7500 8000 8500 7500 8000 8500
2
见表 7。结果显示，不同年型各区域产量趋势检验 实测产量/（kg/hm ）
图 6 模拟产量与实测产量对比
值均小于-2.58（显著性水平 0.01），随着灌水量增
加，产量总体呈显著下降趋势，但枯水年产量变化趋势与总体变化趋势存在差异。

8.6 8.6
Ⅰ区 25%~75% Ⅱ区 25%~75% 1.5IQR 内的范围 Ⅰ区 25%~75% Ⅱ区 25%~75% 1.5IQR 内的范围
中位线 均值 异常值 中位线 均值 异常值
8.4
8.4
8.2
8.2
（t/hm 2 ） （t/hm 2 ） 8.0
产量/ 8.0 产量/ 7.8

7.8
7.6
7.6 7.4
100~200 200~300 300~400 400~500 500~600 100~200 200~300 300~400 400~500 500~600
灌水量/mm 灌水量/mm
（a） 枯水年 （b） 平水年
图 7 Ⅰ区、Ⅱ区不同灌溉情景产量-灌水量关系
表 7 产量 Mann-Kendall 趋势检验值
平水年（P=50%） 枯水年（P=85%）
Ⅰ区 -17.984 1） -12.612 1）
Ⅱ区 -13.491 1） -17.649 1）
注：1）表示 0.01 显著水平。

筛选相同灌水量下各典型年不同区域产量最大的灌溉情景，拟合产量-灌水量关系曲线，结果如
图 8、表 8 所示。结果表明，水稻产量-灌水量响应规律呈非线性关系。灌水量较小时，土壤含水率
较低，作物受到一定程度干旱胁迫，阻碍干物质累积与产量形成，此时增加灌水能够降低水分胁迫
程度，促进产量形成；枯水年水分胁迫更严重，产量形成受到抑制，增加灌水能显著降低水分胁迫
对产量形成的抑制作用。灌水量较大时，土壤常处于饱和状态，土壤含氧量和透气性低，导致水稻
根系发育受阻，进而影响产量形成；灌水量越大，越容易产生深层渗漏，造成无效灌水。因此，随
灌水量增加，水分胁迫逐渐消除，产量为增长趋势，而后影响根系呼吸进而降低产量，但产量整体
仍然呈现随着灌水量增加而降低的趋势。
随着灌水量增加，Ⅰ区最早出现产量降低现象，Ⅱ区较晚出现。原因是地下水埋深小时，地下
水可通过毛管水上升供给水稻需水，此时土壤水分垂向运动为毛管水上升过程，增加灌水量会更早
影响根系呼吸作用，最终导致产量降低；埋深较大时，渗漏增强，因此产量降低现象出现较晚。综
上所述，水稻产量与灌水量响应规律表现出高度非线性，且总体下降趋势明显，并随地下水埋深增
大表现出滞后现象，能够为优化水稻分区灌溉制度提供理论依据。

— 1077 —