Page 9 - 2021年第52卷第9期

介不确定性、未确知性等多种不确定性问题，可从同异反宏观层次、差异度项不断分解的微观层次
开展有关水资源确定性与不确定性的联系和转换分析，得到的分析结果能较好地符合研究问题的实
际情况 ［22］ 。因此，本文以上述各单元水资源供需均衡度作为水资源空间均衡的评价指标，将其与灌
区水资源空间均衡评价等级标准构成一个集对，构造七元联系数以分析二者之间的同异反联系，从
而综合评价计算各种情景下水资源系统的空间均衡等级。

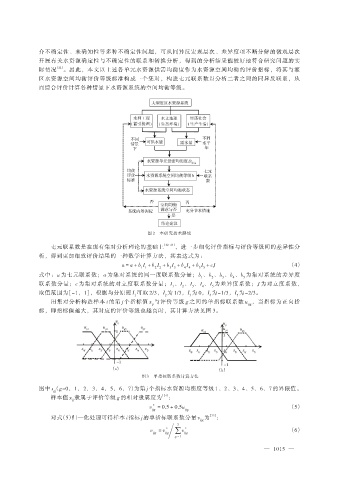
图 2 本研究技术路线

七元联系数是在现有集对分析理论的基础上 ［22-23］ ，进一步细化评价指标与评价等级间的差异性分
析，得到更加细致评价结果的一种数学计算方法，其表达式为：
u = a + b I + b I + b I + b I + b I + cJ （4）
1 1 2 2 3 3 4 4 5 5
式中：u 为七元联系数；a 为集对系统的同一度联系数分量；b 、b 、b 、b 、b 为集对系统的差异度
1 2 3 4 5
联系数分量；c 为集对系统的对立度联系数分量；I 、I 、I 、I 、I 为差异度系数；J 为对立度系数，
1 2 3 4 5
取值范围为［-1，1］，根据均分原理 I 可取 2/3，I 为 1/3，I 为 0，I 为-1/3，I 为-2/3。
1 2 3 4 5
用集对分析构造样本 i 的第 j 个指标值 x 与评价等级 g 之间的单指标联系数 u ，当指标为正向指
ij
ijg
标，即指标值越大，其对应的评价等级也越高时，其计算方法见图 3。

（a） （b）
图 3 单指标联系数计算方法
图中 s（g=0，1，2，3，4，5，6，7）为第 j 个指标水资源均衡度等级 1、2、3、4、5、6、7 的界限值。
gj
样本值 x 隶属于评价等级 g 的相对隶属度为 ［24］ ：
ij
v ∗ = 0.5 + 0.5u （5）
ijg ijg
对式（5）归一化处理可得样本 i 指标 j 的单指标联系数分量 v 为 ［23］ ：
ijg
7
v ijg = v ∗ v ∗ （6）
ijg å ijg
g = 1
— 1015 —