Page 56 - 水利学报2021年第52卷第11期
P. 56
0.29 0.56
0.54
0.27 0.52
y=0.0012x+0.22
2
R =0.55,P<0.01 0.50
NDVI 均值 0.25 NDVI 均值 0.48
0.46
y=0.0018x+0.4493
0.23 0.44
2
R =0.45,P<0.01
0.42
0.21 0.40
1982 1987 1992 1997 2002 2007 2012 2017 1982 1987 1992 1997 2002 2007 2012 2017
年份 年份
(a) 春季 (b) 夏季
0.38
0.36
y=0.0020x+0.2778
0.34 R =0.67,P<0.01
NDVI 均值 0.32
2
0.30
0.28
0.26
1982 1987 1992 1997 2002 2007 2012 2017
年份
(c) 秋季
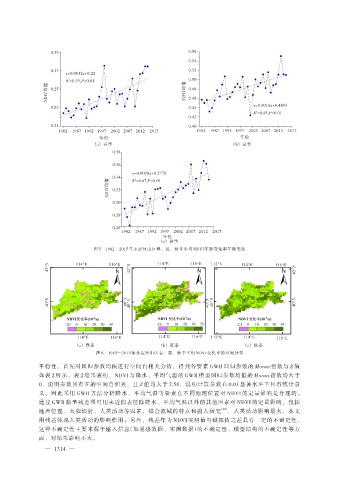
图 5 1982—2015 年永定河山区春、夏、秋季平均 NDVI 年际变化率年际变化
42°N 114°E 116°E 42°N 114°E 116°E 112°E 114°E 116°E 42°N
40°N 40°N 40°N 40°N 40°N 40°N
114°E 116°E 114°E 116°E 112°E 114°E 116°E
(a) 春季 (b) 夏季 (c) 秋季
图 6 1982—2015 年永定河山区春、夏、秋季平均 NDVI 变化率的空间分布
平稳性,首先对回归参数均值进行空间自相关分析,得到各要素 GWR 回归参数的 Moran 指数与 Z 值
如表 2 所示。表 2 结果表明,NDVI 与降水、平均气温的 GWR 模型回归参数均值的 Moran 指数均大于
0,说明参数具有正的空间自相关,且 Z 值均大于 2.58,说明计算参数在 0.01 显著水平下具有统计意
义。因此采用 GWR 方法分析降水、平均气温等要素在不同地理位置对 NDVI 的定量影响是合理的。
通过 GWR 模型残差项可用来近似表征除降水、平均气温以外的其他因素对 NDVI 的定量影响,包括
地理位置、太阳辐射、人类活动等因素,结合流域的特点和前人研究 [28] ,人类活动影响最大,本文
用残差体现人类活动的影响作用;另外,残差作为 NDVI 实测值与模拟值之差具有一定的不确定性,
这种不确定性主要来源于输入信息(如遥感数据、实测数据)的不确定性、模型结构的不确定性等方
面,对结果影响不大。
— 1314 —