Page 113 - 2022年第53卷第2期

)
n (λÑT = h (T amb - T ) （19）
c
式中：n 为渠道边界外法向向量；T 为外界温度，K；T 为边界计算温度，K；h 为对流热交换系
amb c
2
数，W/(m·K)，由风速来近似确定，公式如下：
h = 3.06v + 4.11 （20）
c
式中：v 为风速，m/s；根据现场气象数据，渠顶和渠底风速近似取 5 和 1 m/s，并采用线性函数进行
插值。模型底部为恒温边界，取灌区多年平均温度 8 ℃；模型的左右两边设为绝热边界，即热通量
- n·ÑT = 0。
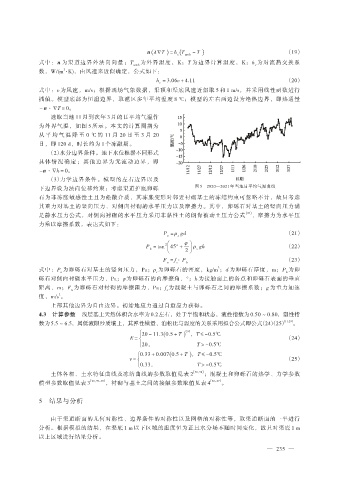
选取当地 11 月到次年 3 月的日平均气温作
为外界气温，如图 5 所示。本文的计算周期为
从 平 均 气 温 降 至 0 ℃ 的 11 月 20 日 至 3 月 20
日，即 120 d，时长约为 1 个冻融期。
（2）水分边界条件。地下水位根据不同形式
具体情况确定；其他边界为无流动边界，即
-n·Ñh = 0。
（3）力学边界条件。模型的左右边界以及
下边界设为法向位移约束；考虑渠道护底卵砾 图 5 2020—2021 年当地日平均气温曲线
石为非冻胀敏感性土且为松散介质，其冻胀变形对邻近衬砌基土的冻结约束可忽略不计，故只考虑
其重力对基土的竖向压力、对侧向衬砌的水平压力以及摩擦力。其中，卵砾石对基土的竖向压力满
足静水压力公式，对侧向衬砌的水平压力采用非黏性土的朗肯被动土压力公式 ［37］ ，摩擦力为水平压
力乘以摩擦系数，表达式如下：
P = ρ gd （21）
s
v
2æ
P = tan ç45° + φ ö ÷ ρ gh （22）
h
è 2 ø s
F = f·P h （23）
s
n
3
式中：P 为卵砾石对基土的竖向压力，Pa；ρ 为卵砾石的密度，kg/m ；d 为卵砾石厚度，m；P 为卵
s
v
h
砾石对侧向衬砌水平压力，Pa；φ为卵砾石的内摩擦角，°；h 为接触面上的各点和卵砾石表面的垂直
距离，m；F 为卵砾石对衬砌的摩擦阻力，Pa；f 为混凝土与卵砾石之间的摩擦系数；g 为重力加速
n
s
2
度，m/s 。
上部其他边界为自由边界。初始地应力通过自重应力获得。
4.3 计算参数 浅层基土天然体积含水率为 0.2左右，处于半饱和状态，液性指数为 0.50 ~ 0.80，塑性指
［11，9］
数为 5.5 ~ 6.5，属低液限沙质壤土，其弹性模量、泊松比与温度的关系采用拟合公式即公式（24）（25） 2 。
ì ï 20 - 11.3(0.5 + T ) ，T  -0.5℃
0.6
E = í （24）
ï
î 20， T > -0.5℃
ì0.33 + 0.007(0.5 + T )，T  -0.5℃
ν = í （25）
î 0.33， T > -0.5℃
［28，38］
土体各相、土水特征曲线及冻结曲线的参数取值见表 2 ；混凝土和卵砾石的热学、力学参数
［28，39-40］ ［26-27］
模型参数取值见表 3 ，衬砌与基土之间的接触参数取值见表 4 。
5 结果与分析

由于渠道断面的几何对称性、边界条件的对称性以及网格的对称性等，取渠道断面的一半进行

分析。根据模拟的结果，在渠底 1 m 以下区域的温度恒为正且水分场不随时间变化，故只对渠底 1 m
以上区域进行结果分析。

— 235 —