Page 110 - 2022年第53卷第2期

此时的变形很小，而受拉侧模袋材料的最大拉应力仅达到 850 kPa，远未达到其比例极限，此为第一
阶段；随着外荷载继续增大至 180 kPa，裂缝继续发展，底部混凝土压应力及模袋拉应力不断增大，
模袋达到比例极限，即 40 MPa，此为第二阶段，如果卸载模袋还具有一定的弹性恢复能力，可以此
为设计阶段；继续加载至 200 kPa 时，混凝土继续开裂，模袋进入非线弹性阶段，应力达到最大抗拉
应力 60 MPa 而断裂破坏。因此，模袋可以显著提高结构的承载能力。
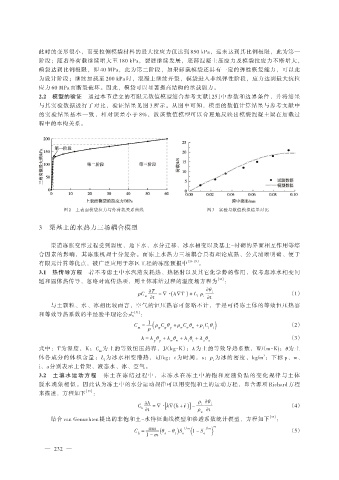
2.2 模型的验证 通过本节建立的有限元数值模型结合参考文献［25］中参数和边界条件，并将结果
与其实验数据进行了对比，验证结果见图 3 所示。从图中可知，模型的数值计算结果与参考文献中
的实验结果基本一致，相对误差小于 8%，故该数值模型可以合理地反映出模袋混凝土梁在加载过
程中的本构关系。

图 2 上表面模袋拉力与外荷载关系曲线 图 3 实验与数值模拟结果对比

3 渠基土的水热力三场耦合模型

渠道冻胀变形过程受到温度、地下水、水分迁移、冰水相变以及基土-衬砌的界面相互作用等综
合因素的影响，其冻胀机理十分复杂。而冻土水热力三场耦合具有理论成熟、公式清晰明确、便于
有限元计算等优点，被广泛应用于寒区工程的冻胀预报中 ［26-29］ 。
3.1 热传导方程 若不考虑土中水汽蒸发耗热、热辐射以及其它化学势的作用，仅考虑冰水相变问
题和固体热传导，忽略对流传热项，则土体冻结过程的温度场方程为 ［30］ ：
)
ρC ∂T = Ñ· (λÑT + L ρ ∂θ i （1）
m ∂t f i ∂t
与土颗粒、水、冰相比较而言，空气的恒压热容可忽略不计，于是可得冻土体的等效恒压热容
和等效导热系数的半经验半理论公式 ［31］ ：
C = ( ρ C θ + ρ C θ + ρ C θ ) （2）
1
m ρ p p p w w w i i i
λ = λ θ + λ θ + λ θ + λ θ （3）
p p w w i i a a
式中：T 为温度，K；C 为土的等效恒压热容，J/（kg·K）；λ为土的等效导热系数，W/（m·K)；θ为土
m
3
体各成分的体积含量；L 为冰水相变潜热，kJ/kg；t 为时间，s；ρ 为冰的密度，kg/m ；下标 p、w、
f i
i、a 分别表示土骨架、液态水、冰、空气。
3.2 土 壤 水 运 动 方 程 冻 土 在 冻 结 过 程 中 ， 未 冻 水 在 冻 土 中 的 饱 和 度 随 负 温 的 变 化 规 律 与 土 体
脱水现象相似。因此认为冻土中的水分运动规律可以用变饱和土的运动方程，即含源项 Richard 方程
来描述，方程如下 ［32］ ：
C ∂h = Ñ∙ [kÑ(h + i ] ) - ρ ∂θ i （4）
i
h ∂t ρ ∂t
w
结合 van Genuchten 提出的非饱和土-水特征曲线模型和渗透系数统计模型，方程如下 ［33］ ：
αm 1 m 1 m ) m
)
C = (θ - θ S ( 1 - S （5）
h 1 - m s r e e
— 232 —