Page 54 - 2023年第54卷第2期

３．３ 输入变量选择 输入变量集合对最终的预测结果有直接的影响，采用偏自相关系数 ＰＡＣＦ识别输
入变量时，在实践中经常依据以下两个标准 ［１０］ ：（１）当滞后 ｔ时刻的变量的 ＰＡＣＦ值超出置信区间时，
选择该变量作为输入；（ ２）当所有的变量都超出置信区间时，选择滞时小的几个变量作为输入。图 ６
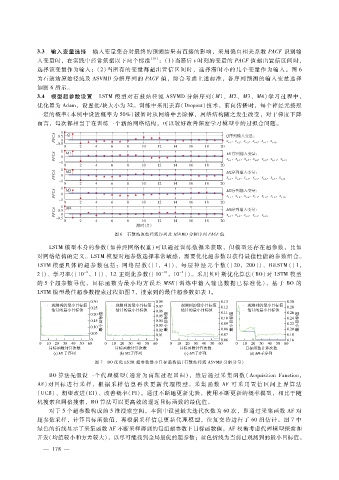
为石鼓站原始径流及 ＡＳＶＭＤ分解序列的 ＰＡＣＦ值，综合考虑上述标准，各序列预测的输入变量选择
如图 ６所示。
３．４ 模型超参数设置 ＬＳＴＭ 模型对石鼓站径流 ＡＳＶＭＤ分解序列（Ｍ１、Ｍ２、Ｍ３、Ｍ４）学习过程中，
优化器为 Ａｄａｍ，设置批?块大小为 ３２。训练中采用丢弃（Ｄｒｏｐｏｕｔ）技术，前向传播时，每个神经元按照
一定的概率（本例中设置概率为 ５０％）被暂时从网络中去除掉，网络结构随之发生改变，对于梯度下降
而言，每次都相当于在训练一个新的网络结构，可以较好改善深度学习模型中的过拟合问题。

图 ６ 石鼓站原始径流序列及 ＡＳＶＭＤ分解序列 ＰＡＣＦ值

ＬＳＴＭ模型本身的参数（如神经网络权重）可以通过训练数据来获取，但模型还存在超参数，比如
对网络结构的定义。ＬＳＴＭ模型对超参数选择非常敏感，需要优化超参数以获得最佳性能的参数组合。
ＬＳＴＭ模型具体 的 超 参 数 包 括：网 络 层 数 （［１，４］）、每 层 神 经 元 个 数 （［２０，２００］）、ＢｉＬＳＴＭ（［１，
－ １０
－ ２
－ ２
２］）、学习率（［１０ ，１］）、Ｌ２正则化参数（［１０ ，１０ ］）。采用贝叶斯优化算法（ＢＯ）对 ＬＳＴＭ 模型
的 ５个超参数 寻 优，目标 函数 为最 小均方 误差 ＭＳＥ（训 练 中 输 入 输 出 数 据 已 标 准 化），基 于 ＢＯ的
ＬＳＴＭ模型最佳超参数搜索过程如图 ７，搜索到的最佳超参数如表 １。

图 ７ ＢＯ优化 ＬＳＴＭ超参数最小目标函数值（石鼓站径流 ＡＳＶＭＤ分解分量）

ＢＯ算法先假设一个代理模型（通常为高斯过程回归），然后通过采集函数（ＡｃｑｕｉｓｉｔｉｏｎＦｕｎｃｔｉｏｎ，
ＡＦ）对目标 进 行 采 样，根 据 采 样 信 息 再 次 更 新 代 理 模 型。采 集 函 数 ＡＦ可 采 用 置 信 区 间 上 界 算 法
（ＵＣＢ）、期望改进（ＥＩ）、改善概率（ＰＩ）。通过不断地更新先验，使用不断更新的概率模型，相比于随
机搜索和网格搜索，ＢＯ算法可以更高效的逼近目标函数的最优值。
对于 ５个超参数构成的 ５维搜索空间，本例中设置最大迭代次数为 ６０次，即通过采集函数 ＡＦ对
超参数采样，计算目标函数值，再根据采样信息更新代理模型，往复交替进行了 ６０组估计。图 ７中
绿色的折线显示了采集函数 ＡＦ不断采样得到的每组超参数下目标函数值，ＡＦ权衡考虑代理模型探索和
开发（均值较小和方差较大），以尽可能找到全局最优的超参数；蓝色折线为当前已观测到的最小目标值。

— １ ７ —
８