Page 102 - 2023年第54卷第6期

达到预设值，存 在 一 个 过 程 （大 约 持 续 １ｈ左 右），
而并非传统意义上的恒温边界，这一过程在模型时
间尺度下是不可忽略的。（２）连续性。从文献［４ － ７］
可知，采用该设备完成的试验，模型表面的温度变
化均是连续的，且都是在有限的 “模型时间” 下模
拟单调地降温或升温过程，无法做到短时间内降温
或升温阶段的切换；为此，结合现场温度数据，采
用正弦或类似函数构建并赋予离心模型试验中的热
边界是较为准确和严谨的做法，但现有的设备和技
术无法实现上述函数的精准构建。（ ３）复杂性。冷热
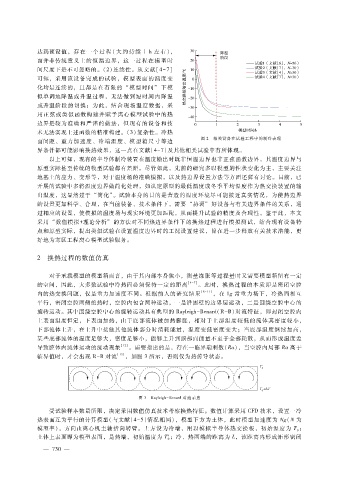
图 ２ 相关设备在试验工程中的制冷表现
面间距、重力加速度、冷端温度、模型箱尺寸等边
界条件都可能影响换热效果，这一点在文献［ ４ － ７］及其他相关试验中有所体现。
以上可知，现有的半导体制冷装置在温度输出时既非恒温边界也非正弦函数边界，其温度边界与
原型实际甚至传统的模型试验都有差距。尽管如此，先前的研究多以模型的性状变化为主，主要关注
地基土的应力、变形等，对于温度场的准确模拟，以及热边界设置方法等方面还鲜有讨论。目前，已
开展的试验中多将温度边界做简化处理，如认定原型的最低温度或冬季平均温度作为热交换装置的输
出温度，这显然过于 “简化”。试验本身的目的是营造的温度环境尽可能接近真实情况，为使热边界
的设置更加科学、合理，在当前装备、技术条件下，需要 “协调” 好设备与有关边界条件的关系，通
过相应的设置，使模拟的温度场与现实环境更加匹配，从而提升试验的精度及合理性。鉴于此，本文
采用 “数值模拟＋ 理论分析” 的方法对不同热边界条件下的换热过程进行模拟测试，结合现有设备特
点和原型实际，提出类似试验在设置温度边界时的工况设置建议，旨在进一步释放有关技术潜能，更
好地为寒区工程离心模型试验服务。

２ 换热过程的数值仿真

对于承载模型的模型箱而言，由于其内部本身狭小，测量冻胀等过程量时又需要模型箱留有一定
的空间，因此，大多数试验中冷热面必须保持一定的距离 ［４ － ７］ 。此时，换热过程的本质即是密闭空腔
内的热交换问题，仅是重力加速度不同。根据前人的研究结果 ［８ － １１］ ，在 １ｇ常重力场下，冷热面相互
平行，密闭空腔两侧绝热时，空腔内包含两种运动，一是沿固壁的边界层运动，二是围绕空腔中心的
旋转运动。其中围绕空腔中心的旋转运动具有典型的 Ｒａｙｌｅｉｇｈ － Ｂｅｎａｒｄ（Ｒ － Ｂ）对流特征，即封闭空腔内
上表面温度恒定，下表面加热，由于底部流体被加热膨胀，相对于上部温度较低的流体其密度较小，
下部流体上升，在上升中接触其他流体部分时消耗能量，温度变低密度变大；当底部温度继续加高，
某些底部流体的温度足够大，密度足够小，能够上升到顶部而能量不至于全部耗散，从而形成温度差
导致腔体内流体运动的流动现象 ［１２］ 。需要指出的是，存在一临界瑞利数（Ｒａ），当空腔内局部 Ｒａ高于
临界值时，才会出现 Ｒ － Ｂ对流 ［１３］ ，如图 ３所示，否则仅为热传导状态。

图 ３ Ｒａｙｌｅｉｇｈ － Ｂｅｎａｒｄ对流示意

受试验样本数量所限，决定采用数值仿真技术考察换热特征。数值计算采用 ＣＦＤ技术，设置一冷
热表面互为平行的计算模型（与文献［ ４ － ５］情况相同），模型下方为土体，此时模型加速度为 Ｎｇ（Ｎ为
模型率），方向由离心机主轴指向转臂。上方设为冷端，用以模拟半导体热交换板，初始温度为 Ｔ；
０
土体上表面即为模型表面，是热端，初始温度为 Ｔ′；冷、热两端的距离为 Ｌ，该距离内形成矩形密闭
０
— ７ ３ —
０