Page 105 - 2023年第54卷第6期

标是冻结指数，根据其定义 ［１６］ ，以模型表面 ０～ － １０℃这一阶段为例，对图 ５所示工况计算冻结指数，
２
按同一间距进行归类，其中时间比尺按原型：模型 ＝ Ｎ换算 ［１７］ 。需要说明的是，由于冻结指数是将低
于 ０℃的天数乘以日均气温并求和得出，考虑到模拟工况中进入负温后模型表面的温度是持续下降
的，且都为负温，故有关工况中的冻结指数就是温度拟合函数对原型时间的定积分（如图 ８），作为区
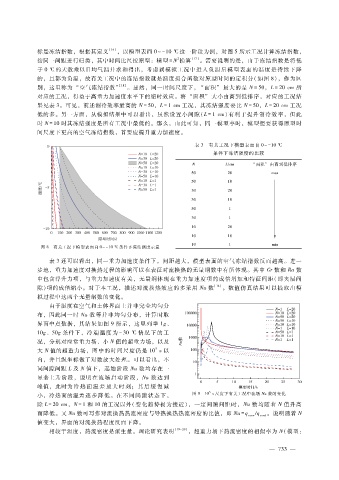
别，这里称为 “空气冻结指数” ［１８］ 。显然，同一时间尺度下， “面积” 最大的是 Ｎ＝ ５０ ，Ｌ ＝ ２０ｃｍ所
对应的工况，得益于高重力加速度水平下的缩时效应。将 “面积” 大小由高到低排序，对应的工况结
果见表 ３。可见，前述制冷效率最高的 Ｎ＝ ５０ ，Ｌ ＝ １ｃｍ工况，其冻结强度要比 Ｎ＝ ５０ ，Ｌ ＝ ２０ｃｍ工况
低的多。另一方面，从模拟结果中可以看出，虽然设置小间隙（ Ｌ ＝ １ｃｍ ）有利于提升制冷效率，但此
时 Ｎ ＝ １０ 时其冻结强度是所有工况中最低的。那么，由此可知，同一模型率时，模型想要获得原型时
间尺度下更高的空气冻结指数，首要应提升重力加速度。

表 ３ 有关工况下模型表面自 ０～ － １０℃
条件下冻结强度的比较

Ｎ Ｌ?ｃｍ “面积” 由高到低排序
５０ ２０ ｍａｘ
５０ １０
３０ ２０
３０ １０
５０ １
３０ １
１０ ２０
１０ １０
１０ １ ｍｉｎ
图 ８ 有关工况下模型表面自 ０～ － １０℃条件下冻结强度示意

表 ３还可以看出，同一重力加速度条件下，间距越大，模型表面的空气冻结指数反而越高。进一
步地，重力加速度对换热过程的影响可以在表征对流换热的无量纲数中有所体现。其中 Ｇｒ数和 Ｒａ数
中包含浮升力项，与重力加速度有关，无量纲体现在重力加速度项的成倍增加和特征间距（即夹层间
隙）项的成倍缩小。对于本工况，描述对流换热效应的多采用 Ｎｕ数 ［１４］ 。数值仿真结果可以提取出模
拟过程中这两个无量纲数的变化。
由于温度在空气和土体界面上并非完全均匀分
布，因此同一时 Ｎｕ数等并非均匀分布，计算时取
界面中点数据，其结果如图 ９所示，这里列举 １ｇ、
１０ｇ、５０ｇ条件下，冷 端温度 为 － ３０℃ 情况 下的工
况，分别对应常重力场、小 Ｎ值的超重力场，以及
５
大 Ｎ值的超重力场，图中的时间尺度仍是 １０ ｓ以
内，并且纵坐标做了对数放大处理。可以看出，不
同间隙间距 Ｌ及 Ｎ值下，起始阶段 Ｎｕ数均存在一
显著上升阶段，说明在流场启动阶段，Ｎｕ数达到
峰值，此时为 冷 热 面 温 差 最 大 时 刻；其 后 缓 慢 减
５
小，冷热面的温差逐步降低。在不同间隙状态下， 图 ９ １０ ｓ尺度下有关工况中流场 Ｎｕ数的变化
除 Ｌ ＝ ２０ｃｍ ，Ｎ ＝ １ 和 １０的工况以外（变化趋势极为接近），一定间隙间距时，Ｎｕ数均随着 Ｎ值升高
而降低。又 Ｎｕ数可写作对流换热热流密度与导热换热热流密度的比值，即 Ｎｕ ＝ ｑ ?ｑ 。说明随着 Ｎ
ｃｏｎｄ
ｃｏｎｖ
值变大，界面的对流换热程度反而下降。
相较于温度，热流密度是派生量。理论研究表明 ［１９ － ２０］ ，超重力场下热流密度的相似率为 Ｎ（模型：

— ７ ３ ３ —