Page 25 - 2024年第55卷第1期

表 ５ 动力计算模型参数
ｎ′ ｃ １ ?％ ｃ ４ ?％
ｋ １ ｋ ２ λ ｍａｘ ｃ ２ ｃ ３ ｃ ５
反滤 １４．５０ １３５６ ０．３１２ ０．２３ ０．３２ ０．６３ ０ ８．４５ ０．７５
过渡 １５．７０ １９９７ ０．３２８ ０．２２ ０．５６ ０．４２ ０ ８．２５ ０．４０
堆石 １８．２５ ２３１２ ０．２７３ ０．２０ ０．７１ ０．６５ ０ ９．２２ ０．３７
心墙 ２１．３５ １１０６ ０．５５６ ０．２５ ０．０４ ０．１７ ０ １８．９０ １．０２

４．２．２ 土石坝地震需求模型建立与分析 采用参数优化器 Ｈｙｐｅｒｏｐｔ实现 ＴＰＥ算法对 ＭＬＰ神经网络超
参数的优化。首先，初始化 Ｈｙｐｅｒｏｐｔ参数，最小化目标为模型均方误差；最大迭代次数为 ５００，搜索
算法为 ｔｐｅ．ｓｕｇｇｅｓｔ。其次，设置多层感知机神经网络的初始参数，隐藏层数量为 ２，隐藏层神经元数量
搜索空间为 ４～１０２４，激活函数搜索空间为 ｔａｎｈ、ｓｉｇｍｏｉｄ、ｒｅｌｕ，学习率搜索空间为 ０．００００１～０．１。最
后，随机选取 １１４０组地震动－ 坝顶沉降样本作为训练集对 ＴＰＥ － ＭＬＰ模型进行训练，剩余的 ３８１组样
本作为测试集测试 ＴＰＥ － ＭＬＰ模型的性能。经 ＴＰＥ优化 ＭＬＰ最优超参数为隐藏层神经元数 １２８ × ５１２，
学习率 ０．００００５，激活函数 ｒｅｌｕ。
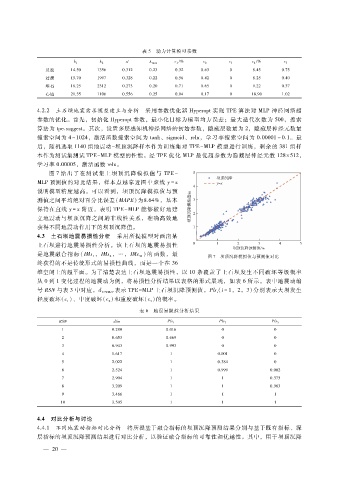
图 ７给 出 了在 测试 集上 坝顶 沉降 模拟 值 与 ＴＰＥ －

ＭＬＰ预测值的对比结果，样本点越靠近图中虚线 ｙ ＝ ｘ
说明模型精度越高。可以看到，坝顶沉降模拟值与预
测值之间平均绝对百分比误差（ ＭＡＰＥ）为８．６４％，基本
保持在直线 ｙ ＝ ｘ附近，表明 ＴＰＥ － ＭＬＰ能够较好地建
立地震动与坝顶沉降之间的非线性关系，准确高效地
获得不同地震动作用下的坝顶沉降值。
４．３ 土石坝地震易损性分析 采用所提模型对西南某
土石坝进行地震易损性分析。该土石坝的地震易损性
是地震融合指标（ ＩＭｓ，ＩＭｓ，…，ＩＭｓ）的函数，最
１ ２ ３６ 图 ７ 坝顶沉降模拟值与预测值对比
终获得的不是传统形式的易损性曲线，而是一个在 ３６
维空间上的超平面。为了清楚表达土石坝地震易损性，以 １０条覆盖了土石坝发生不同破坏等级概率
从 ０到 １变化过程的地震动为例，将易损性分析结果以表格的形式展现，如表 ６所示。表中地震动编
号 ＲＳＮ与表 ３中对应，ｄ 表示 ＴＰＥ － ＭＬＰ土石坝沉降预测值，Ｐｌｓ（ｉ ＝ １ ，２，３）分别表示大坝发生
ＴＰＥＭＬＰ ｉ
轻度破坏（ ｃ）、中度破坏（ｃ）和重度破坏（ｃ）的概率。
１ ２ ３
表 ６ 地震易损性分析结果
ＲＳＮ ｄ?ｍ Ｐｌｓ １ Ｐｌｓ ２ Ｐｌｓ ３
１ ０．２８０ ０．０１６ ０ ０
２ ０．６５３ ０．６６９ ０ ０
３ ０．９４３ ０．９９３ ０ ０
４ １．６１７ １ ０．００１ ０
５ ２．０２２ １ ０．３８４ ０
６ ２．５２４ １ ０．９９９ ０．００２
７ ２．９０４ １ １ ０．３７５
８ ３．２０９ １ １ ０．９６３
９ ３．４６６ １ １ １
１０ ３．５０５ １ １ １

４．４ 对比分析与讨论
４．４．１ 不同地震动指标对比分析 将所提基于融合指标的坝顶沉降预测结果分别与基于既有指标、深
层指标的坝顶沉降预测结果进行对比分析，以验证融合指标的可靠性和优越性。其中，用于坝顶沉降

— ２ ０ —