Page 23 - 2024年第55卷第1期

{ ｌ（ｘ） ｙ＜ｙ 
ｐ（ｘ｜ｙ） ＝ ｇ（ｘ） ｙ ≥ｙ  （６）


进而基于贝叶斯定理和 γ ＝ Ｐ（ｙ＜ｙ ）可推得 Ｐ ｘ 表达式如下：
()
Ｐ（ｘ） ＝ γ ｌ（ｘ） ＋ （１ － γ ）ｇ（ｘ） （７）
最后基于 Ｐ（ｘｙ）和 Ｐ（ｘ）表达式，可对 ＥＩ进行如下变形：
ｙ 
∫  － １
（ｙ －ｙ）Ｐ（ｙ）ｄｙ
(
－ ! ｇ（ｘ）
ＥＩ （ｘ） ＝ ∝ γ＋（１－γ ） ) （８）
ｙ
ｇ（ｘ） ｌ（ｘ）
γ＋（１－γ ）
ｌ（ｘ）
由式（８）可知，在每次迭代过程中，通过最小化比值
ｇ（ｘ）?ｌ（ｘ）取得最大化的 ＥＩ值，从而获得最优的 ＭＬＰ超
参数组合。
采用数值模拟方法获得不同地震动作用下的土石坝
响应，建立土石 坝 地 震 响 应 样 本 数 据 集，进 而 对 ＴＰＥ －
ＭＬＰ神经网络进行训练，构建基于 ＴＰＥ － ＭＬＰ的土石坝地
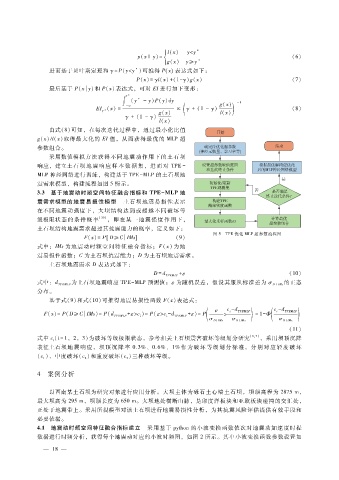
震需求模型，构建流程如图 ５所示。
３．３ 基于地震动时频空间特征融合指标和 ＴＰＥ － ＭＬＰ地
震需求模型的地震易损性模型 土石坝地震易损性表示
在不同地震动强度下，大坝结构达到或超越不同破坏等
级极限状态的条件 概率 ［３０］ ，即 在某 一地震 强度作 用 下，
土石坝结构地震需求超过其抗震能力的概率，定义如下：
图 ５ ＴＰＥ优化 ＭＬＰ超参数流程图
Ｆ（ｘ） ＝Ｐ Ｄ ≥Ｃ ＩＭｓ ] （９）
[
式中：ＩＭｓ为地震动时频空间特征融合指标；Ｆ（ｘ）为地
震易损性函数；Ｃ为土石坝抗震能力；Ｄ为土石坝地震需求。
土石坝地震需求 Ｄ表达式如下：
Ｄ ＝ ｄ ＴＰＥＭＬＰ ε （１０）
＋
式中：ｄ ＴＰＥＭＬＰ 为土石坝地震响应 ＴＰＥ － ＭＬＰ预测值；ε 为随机误差，假设其服从标准差为 σ Ｄ｜ＩＭｓ 的正态
分布。
基于式（９）和式（１０）可推得地震易损性函数 Ｆ（ｘ）表达式：
( ε ｃ － ｄ ＴＰＥＭＬＰ ) ( ｃ － ｄ ＴＰＥＭＬＰ )
ｉ
ｉ
＋
ＴＰＥＭＬＰ ε ＞ｃ） ＝Ｐ（ ε ＞ｃ － ｄ
Ｆ（ｘ） ＝Ｐ（Ｄ ≥Ｃ ＩＭｓ） ＝Ｐ（ｄ ＋ ｉ ｉ ＴＰＥＭＬＰ ε ） ＝Ｐ ＞ ＝ １ － Φ
σ Ｄ｜ＩＭｓ σ Ｄ｜ＩＭｓ σ Ｄ｜ＩＭｓ
（１１）
式中 ｃ（ｉ ＝ １ ，２，３）为破坏等级极限状态，参考相关土石坝震害破坏等级划分研究 ［６，７］ ，采用坝顶沉降
ｉ
表征土石坝 地 震 响 应，坝 顶 沉 降 率 ０．３％、０．６％、１％作 为 破 坏 等 级 划 分 标 准，分 别 对 应 轻 度 破 坏
（ ｃ）、中度破坏（ｃ）和重度破坏（ｃ）三种破坏等级。
１ ２ ３
４ 案例分析

以西南某土石坝为研究对象进行应用分析。大坝主体为砾石土心墙土石坝，坝顶高程为 ２８７５ｍ，
最大坝高为 ２９５ｍ，坝顶长度为 ６５０ｍ。大坝地处横断山脉，是印度洋板块和亚欧板块碰撞的交汇处，
正处于地震带上。采用所提模型对该土石坝进行地震易损性分析，为其抗震风险评估提供有效手段和
必要依据。
４．１ 地震动时频空间特征融合指标建立 采用基于 ｐｙｔｈｏｎ的小波变换函数依次对地震动加速度时程
数据进行时频分析，获得每个地震动对应的小波时频图，如图 ２所示。其中小波变换函数参数设置如

— １ ８ —