Page 113 - 2024年第55卷第8期

梁系组成的受力体系，共同承受荷载并满足变位协调条件。设计实践中，水平拱的个数应能够反映主
要的河谷地形地质条件，一般地，拱体系中的水平拱个数 ｎ取值 ８～１０，梁数则相应地为 ２ｎ － １ 。
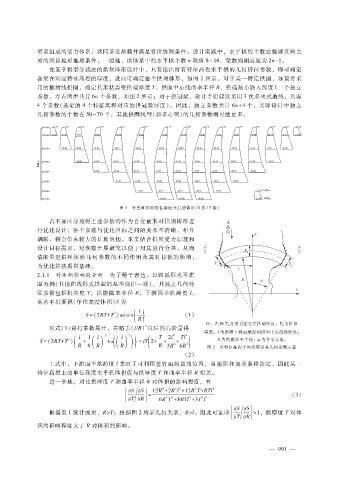
在基于拱梁分载法的拱坝体形设计中，只要给出所有特征高程水平拱的几何特征参数，即可确定
各梁在对应特征高程的厚度，进而可确定整个拱坝体形，如图 １所示。对于某一特定拱圈，如最常采
用的抛物线拱圈，确定其形状需要拱端厚度 Ｔ、拱圈中心线曲率半径 Ｒ、拱端最小嵌入深度 ｌ三个独立
参数，左右两岸共计 ６ｎ个参数，如图 ２所示；对于拱冠梁，设计手册建议采用 ３次多项式曲线，共需
４个参数（选定的 ４个特征高程对应的拱冠梁厚度）。因此，独立参数共计 ６ｎ ＋ ４个，实际设计中独立
几何参数的个数在 ５０～７０个，其他拱圈线型（如多心圆）的几何参数则可能更多。

图 １ 叶巴滩拱坝沿各梁展开后的体形（８拱 １５梁）

若不加区分地将上述参数均作为自变量来对拱坝体形进
行优化设计，各个参数与优化目标之间的关系不清晰，相互
耦联，将会带来较大的计算负担。本文结合拱坝受力原理和
设计目标需求，对参数开展研究以便于对其进行分类，从而
清晰界定拱坝体形几何参数的不同作用及其对目标的影响，
为优化算法提供基础。
２．１．１ 对体积影响的分析 为了便于表达，以圆弧形水平拱
圈为例（其他曲线形式拱圈的基本规律一致），其独立几何特
征参数包括拱厚度 Ｔ，拱腹曲率半径 Ｒ，下游面半拱跨度 ｌ，
其水平拱面积（单位高度体积） Ｓ为
ｌ
( )
２
Ｓ ＝ （２ＲＴ ＋ Ｔ）ａｒｃｓｉｎ Ｒ （１）
注：Ｔ １ 和 Ｔ ２ 分别为左右岸拱端厚度；Ｔ ０ 为拱顶
３
对式（１）进行泰勒展开，并略去（ｌ?Ｒ）以后的高阶量得
厚度；ｌ为拱圈下游面端点到拱坝中心线的距离；
２
２
３
３
Ｔ ２ ｌ Ｔｌ
ｌ １ ｌ
ｌ
( ) ( ))) (
(
Ｒ为拱腹曲率半径；φ为半中心角。
２
＋
Ｓ ＝ （２ＲＴ ＋ Ｔ） ( Ｒ ６ Ｒ ＋ ｏ Ｒ ＝ ｌＴ２ ＋ ＋ ２ ＋ ３ ) 图 ２ 某特征高程平面拱圈及其几何参数示意
Ｒ ３Ｒ ６Ｒ
（２）
上式中，下游面半拱跨度 ｌ表征了可利用基岩面的最浅位置，由地形和地质条件决定，因此某一
特征高程上的单位高度水平拱体积仅与拱厚度 Ｔ和曲率半径 Ｒ相关。
进一步地，对比拱厚度 Ｔ和曲率半径 Ｒ对体积的影响程度，有
３
２
２ ２
４
 Ｓ  Ｓ １２Ｒ＋ ２ Ｒｌ ＋ １２ ＲＴ ＋ ＲＴｌ
＝ （３）
２ ２
２ ２
 Ｔ  Ｒ ６ＲＴ＋ ８ ＲＴｌ ＋ ３ Ｔｌ
２
 Ｓ  Ｓ
根据表 １统计成果，Ｒ＞Ｔ；根据图 ２所示几何关系，Ｒ＞ｌ。因此可证明 ＞１，拱厚度 Ｔ对体
 Ｔ  Ｒ
积的影响程度大于 Ｒ对体积的影响。
— ９ ９ １ —